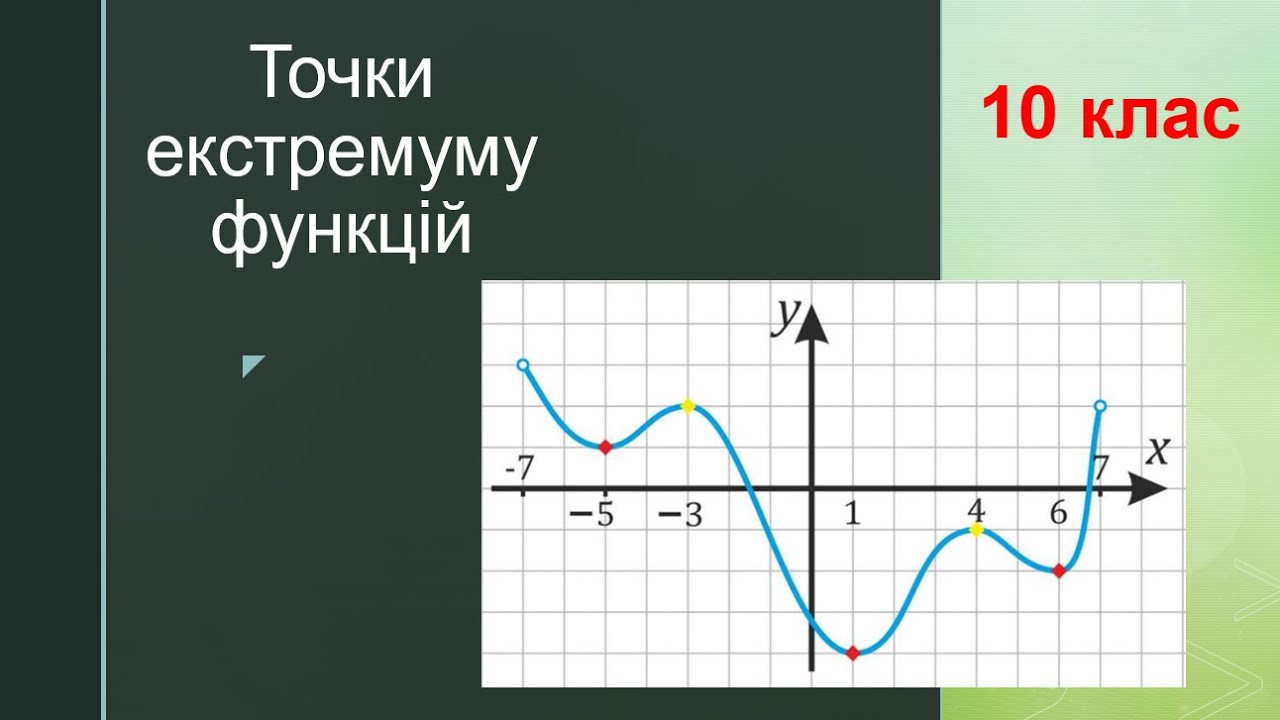
Коли функція досягає свого піку або дна, ніби гірська вершина чи глибока долина на графіку, саме там ховається точка екстремуму. Це місце, де значення функції стає найбільшим чи найменшим у певній околиці, і розуміння цього відкриває двері до аналізу поведінки кривих у реальному світі. Уявіть, як інженери оптимізують траєкторію ракети чи економісти прогнозують ринкові коливання – все починається з цих критичних точок.
Точка екстремуму не просто абстрактне поняття; вона пульсує в серці диференціального числення, дозволяючи нам розбирати функції на частини. Локальний максимум нагадує момент тріумфу, коли функція піднімається вище за сусідів, а мінімум – це тиха гавань спокою серед бурхливих змін. Без цих точок математика втратила б свій інструментарій для моделювання реальності, від фізики до біології.
Визначення точки екстремуму: основи та нюанси
Точка екстремуму функції – це значення аргументу, де функція набуває локального максимуму чи мінімуму. Згідно з класичним визначенням, якщо для функції f(x) в точці x0 існує околиця, де f(x) ≤ f(x0) для максимуму або f(x) ≥ f(x0) для мінімуму, то x0 стає тією самою точкою. Це не завжди глобальний рекорд, а радше локальний герой у своєму маленькому світі.
Розрізняють локальні та глобальні екстремуми: локальний обмежується невеликою ділянкою, тоді як глобальний панує над усім доменом. Наприклад, на інтервалі [a, b] глобальний максимум може ховатися на кінцях чи в критичних точках всередині. Ця відмінність стає ключовою, коли ми аналізуємо функції з кількома “вершинами”, ніби гірський ланцюг з різними піками.
У математичних термінах, точка x0 є точкою локального максимуму, якщо існує δ > 0 таке, що для всіх x у (x0 – δ, x0 + δ) виконується f(x) ≤ f(x0). Аналогічно для мінімуму. Ці визначення, витягнуті з основ диференціального аналізу, дозволяють точно класифікувати поведінку функцій, роблячи їх передбачуваними інструментами в руках вчених.
Локальний vs глобальний екстремум: детальний розбір
Локальний екстремум обмежується околицею, де функція не виходить за межі свого “локального чемпіонства”. Уявіть графік синусоїди: кожен пік – локальний максимум, але глобальний залежить від розглядуваного інтервалу. Глобальний екстремум, навпаки, є абсолютним лідером на всьому домені, ігноруючи дрібні коливання.
У реальних задачах ця різниця критична; наприклад, в оптимізації прибутку компанії локальний максимум може бути пасткою, якщо глобальний ховається далі. Математики використовують теореми, як теорема Вейєрштрасса, щоб гарантувати існування глобальних екстремумів на компактних множинах. Це додає впевненості в розрахунках, перетворюючи абстракцію на практичний інструмент.
Як знайти точку екстремуму: методи та алгоритми
Щоб відшукати точку екстремуму, починаємо з похідної: в критичних точках похідна дорівнює нулю або не існує. Для функції f(x) розв’язуємо рівняння f'(x) = 0, а потім перевіряємо знак похідної навколо. Це ніби сканування ландшафту в пошуках вершин і долин.
Перша похідна вказує на монотонність: якщо f'(x) змінює знак з плюса на мінус, то це максимум, і навпаки для мінімуму. Друга похідна додає точності – якщо f”(x) > 0, то мінімум, а якщо < 0 – максимум. Ці тести, розроблені століттями математичного прогресу, роблять процес систематичним і надійним.
Для функцій багатьох змінних справа ускладнюється: шукаємо часткові похідні і розв’язуємо систему рівнянь. Матриця Гессе допомагає класифікувати точки, визначаючи, чи це сідлова точка чи справжній екстремум. Уявіть багатовимірний простір, де екстремуми ховаються в невидимих долинах – математика освітлює шлях.
Приклади знаходження точок екстремуму
Візьмімо просту функцію f(x) = x². Похідна f'(x) = 2x = 0 при x=0, і друга похідна f”(0)=2>0, тож це мінімум. Графік параболи відкривається вгору, і точка (0,0) – дно цієї “чаші”.
Інший приклад: f(x) = x³ – 3x. Похідна 3x² – 3 = 0 дає x=±1. При x=1 друга похідна негативна – максимум, при x=-1 позитивна – мінімум. Це ілюструє, як функція може мати обидва типи екстремумів, ніби хвиляста дорога з підйомами та спусками.
Для багатьох змінних: f(x,y) = x² + y². Часткові похідні 2x=0 і 2y=0 дають (0,0), а Гессе підтверджує мінімум. Це класична “параболоїдна чаша”, де екстремум – центр.
Застосування точок екстремуму в реальному житті
У фізиці точки екстремуму моделюють траєкторії частинок, де мінімум енергії визначає стабільні стани. Економісти використовують їх для максимізації прибутку, розв’язуючи задачі на умовний екстремум з обмеженнями. Біологія застосовує концепцію в моделях популяцій, де екстремуми вказують на точки рівноваги.
У машинному навчанні алгоритми градієнтного спуску шукають мінімуми функцій втрат, оптимізуючи нейронні мережі. Це ніби тренування моделі, де кожен крок наближає до ідеальної “долини” точності. Навіть у повсякденному житті, плануючи маршрут, ми інтуїтивно шукаємо мінімум відстані чи часу.
Сучасні приклади включають оптимізацію логістики: компанії як Amazon використовують алгоритми для мінімізації витрат на доставку, знаходячи екстремуми в складних функціях. У медицині моделі поширення хвороб знаходять піки інфекцій, допомагаючи прогнозувати спалахи.
Умовний екстремум: коли є обмеження
Метод Лагранжа перетворює задачу з обмеженнями на пошук екстремумів нової функції. Для f(x,y) з обмеженням g(x,y)=c розв’язуємо ∇f = λ∇g. Це елегантно розплутує вузли, ніби ключ до замка.
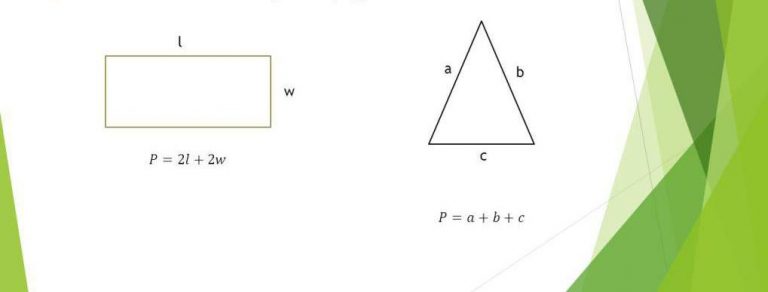
Приклад: максимізувати площу прямокутника з фіксованим периметром. Функція A=xy з 2x+2y=P дає максимум при квадраті. Це демонструє, як математика оптимізує ресурси.
Типові помилки при роботі з точками екстремуму
🚫 Змішування локального та глобального: Багато новачків думають, що знайдений максимум – абсолютний, але на нескінченному домені глобальний може не існувати, як у функції y=x, яка росте без меж.
🚫 Ігнорування кінців інтервалу: У закритих інтервалах екстремуми часто на краях, а не тільки в критичних точках – забуваючи перевірити, втрачаєш справжній пік.
🚫 Неправильне використання другої похідної: Якщо f”(x0)=0, тест не працює, і потрібні інші методи, як перевірка знаку першої похідної, інакше висновки хибні.
🚫 Для багатьох змінних: Забувати про сідлові точки, де Гессе невизначена, може призвести до помилкової класифікації, ніби плутанина в лабіринті.
Ці помилки часто виникають через поспіх, але повільний аналіз з графіками рятує ситуацію. Експерти радять завжди візуалізувати функцію, щоб інтуїція підкріплювала розрахунки.
Практичні приклади та вправи для освоєння
Спробуйте f(x)=sin(x): критичні точки при x=π/2 + kπ, де чергуються максимуми та мінімуми. Це ідеально для розуміння періодичних функцій. Інший: f(x)=e^{-x²}, гаусіан, з максимумом при x=0.
Для вправ: знайдіть екстремуми f(x)=x^4 – 4x². Похідна 4x³-8x=0 дає x=0, ±√2; перевірка показує мінімуми при ±√2 і максимум при 0. Це вчить розпізнавати “подвійні” екстремуми.
У багатьох змінних: f(x,y)=xy – x – y. Часткові дають критичну точку (1,1), яка є сідловою. Такі приклади загострюють навички, роблячи теорію живою.
Таблиця порівняння методів знаходження екстремумів
Ось порівняння основних методів для різних типів функцій:
| Метод | Застосування | Переваги | Недоліки |
|---|---|---|---|
| Тест першої похідної | Одновимірні функції | Простота, показує монотонність | Не завжди визначає тип |
| Тест другої похідної | Гладкі функції | Швидка класифікація | Не працює при f”=0 |
| Метод Лагранжа | З обмеженнями | Обробляє умови | Складніша обчислювально |
| Гессіан | Багатовимірні | Повна класифікація | Вимагає матриць |
Ця таблиця базується на стандартних математичних підходах, описаних у джерелах як Вікіпедія та освітні сайти на кшталт miyklas.com.ua. Вона допомагає обрати метод залежно від задачі, спрощуючи вибір.
Історія розвитку поняття екстремуму
Концепція екстремумів сягає часів Ньютона та Лейбніца, які заклали основи диференціального числення. Ферма в 17 столітті вже шукав максимуми для оптичних задач. Пізніше Лагранж розвинув методи для обмежень, революціонізувавши оптимізацію.
У 20 столітті, з комп’ютерами, чисельні методи як градієнтний спуск стали нормою. Сьогодні, в 2025 році, квантові обчислення обіцяють прискорити пошук екстремумів у величезних просторах, ніби стрибок у майбутнє математики.
Ця еволюція відображає, як абстрактні ідеї перетворюються на інструменти, що змінюють світ, від промисловості до штучного інтелекту.
Сучасні виклики та перспективи
У еру великих даних екстремуми в високовимірних просторах стають складними, вимагаючи алгоритмів на кшталт генетичних. Проблеми як “прокляття розмірності” ускладнюють пошук, але машинне навчання долає бар’єри.
У кліматичних моделях екстремуми прогнозують екстремальні події, допомагаючи боротися зі змінами. Майбутнє обіцяє інтеграцію з AI, де екстремуми оптимізують все від трафіку до персоналізованої медицини.
Захоплює, як ці точки, народжені в математиці, тепер керують технологічним прогресом, роблячи світ ефективнішим і передбачуванішим.