Неправильний дріб, де чисельник перевищує знаменник, часто з’являється в повсякденних розрахунках, ніби ховаючи в собі цілу частину, готову вирватися назовні. Ця математична форма, наче переповнена склянка, потребує перетворення в мішане число, щоб стати зручнішою для розуміння – з чіткою цілою частиною та залишковим дробом. Уявіть, як ви ділите піцу на шматки, де загальна кількість перевищує одну цілу, і ось ви вже маєте рецепт для перетворення, який робить числа живими та застосовними.
Процес починається з базового розуміння: неправильний дріб, наприклад, 7/3, означає сім частин, розділених на три, що перевищує одиницю. Перетворюючи його, ми виділяємо цілі трійки та залишок, перетворюючи на 2 і 1/3 – ніби розкладаємо хаос на акуратні полиці. Такий підхід не просто механічний; він відкриває двері до глибшого сприйняття дробів у реальному житті, від кулінарії до інженерії.
Що таке неправильний дріб і чому його перетворюють
Неправильний дріб – це коли чисельник більший або дорівнює знаменнику, наче число виходить за межі простої частки. Взяти хоча б 5/2: п’ять половинок перевищують дві цілі, створюючи ефект надлишку. Такі дроби часто виникають у розрахунках, де потрібно точно вимірювати, але для повсякденного використання вони менш інтуїтивні, ніж мішані числа.
Перетворення допомагає візуалізувати кількість, роблячи її ближчою до реальності – уявіть, як ви міряєте тканину для штор, і 13/4 метри легше сприймається як 3 метри і 1/4. За даними математичних ресурсів, цей метод походить з давніх часів, коли єгиптяни використовували дроби для будівництва пірамід, перетворюючи їх для точності. Сьогодні він незамінний у шкільній програмі, де учні вчаться бачити за цифрами справжні величини.
Але чому саме перетворювати? Бо мішане число робить абстрактне конкретним, ніби переводить іноземну мову на рідну. Воно складається з цілої частини та правильного дробу, де знаменник завжди більший за чисельник залишку, забезпечуючи баланс і ясність.
Крок за кроком: базовий алгоритм перетворення
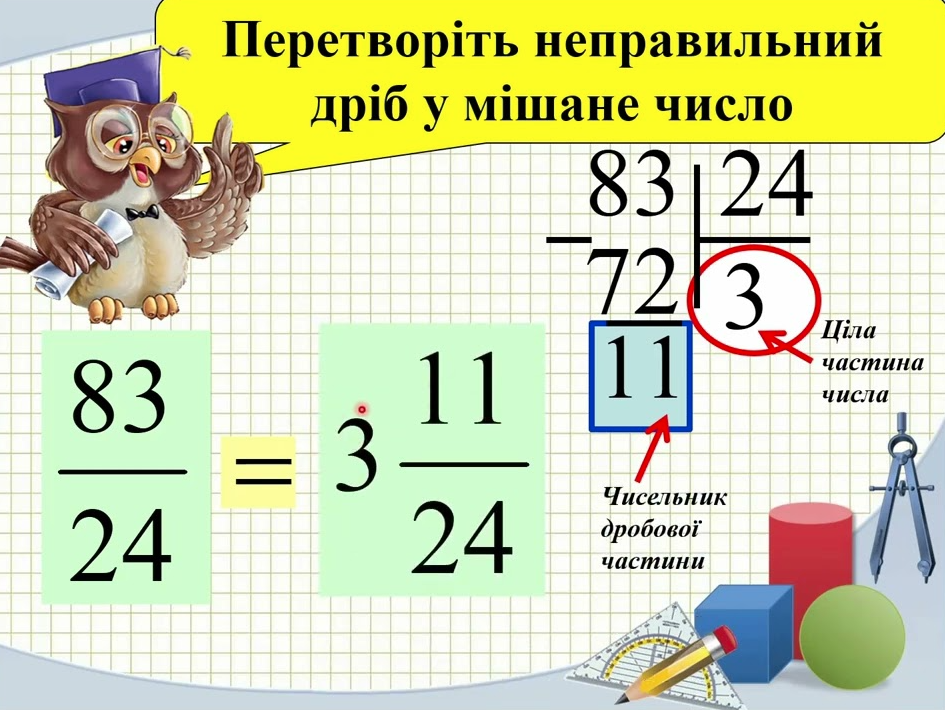
Розпочніть з ділення чисельника на знаменник – це серце процесу, ніби розрізаєте яблуко, щоб побачити, скільки цілих частин ховається всередині. Для дробу 17/5 поділіть 17 на 5: виходить 3 з остачею 2, тож мішане число – 3 2/5. Ця операція проста, але вимагає уваги до деталей, щоб уникнути плутанини з остачами.
Далі запишіть цілу частку як основу, а остачу – як чисельник нового дробу зі старим знаменником. Якщо остача нульова, як у 10/2, то виходить просто ціле число 5 – чисте і без зайвих шматочків. Такий метод працює для будь-яких позитивних дробів, роблячи його універсальним інструментом.
- Визначте чисельник і знаменник: для 9/4 чисельник 9, знаменник 4.
- Поділіть чисельник на знаменник: 9 ÷ 4 = 2 з остачею 1, бо 4 × 2 = 8, а 9 – 8 = 1.
- Сформуйте мішане число: 2 1/4, де 2 – ціла частина, 1/4 – дробова.
- Перевірте: помножте цілу частину на знаменник і додайте чисельник – має вийти оригінальний чисельник.
Ці кроки, ніби рецепт улюбленої страви, стають інтуїтивними з практикою, дозволяючи швидко перетворювати навіть складні дроби. Пам’ятайте, для від’ємних дробів, як -7/3, перетворення дає -2 1/3, зберігаючи знак перед цілою частиною для точності.
Приклади з реального життя: від кухні до будівництва
На кухні неправильні дроби з’являються часто – уявіть рецепт, де потрібно 11/4 склянки борошна: перетворивши на 2 3/4, ви легко відміряєте дві повні склянки і три чверті. Це не просто цифри; це спосіб уникнути помилок, роблячи приготування їжі приємним процесом. У будівництві, скажімо, 25/6 метрів кабелю стає 4 1/6, допомагаючи точно планувати матеріали без зайвих витрат.
Ще один приклад з фінансів: якщо ви розраховуєте відсотки, 19/8 відсотка прибутку перетворюється на 2 3/8, роблячи аналіз зрозумілішим для інвесторів. Такі перетворення, за даними освітніх платформ, полегшують навчання, дозволяючи учням пов’язувати математику з щоденними завданнями. А в спорті, вимірюючи дистанції, 13/5 кілометрів стає 2 3/5, мотивуючи бігунів бачити прогрес чітко.
Ці приклади показують, як перетворення робить абстрактне відчутним, ніби перетворює туман на ясний день. Воно додає впевненості, дозволяючи застосовувати математику без страху перед складними формами.
Складніші приклади з великими числами
Для більших дробів, як 123/7, ділення дає 17 з остачею 4, тож 17 4/7 – ніби розкладаєте велику мозаїку на частини. Тут ключ у точному діленні: 7 × 17 = 119, 123 – 119 = 4. Якщо знаменник великий, як у 456/13, результат 35 1/13 вимагає терпіння, але винагороджує ясністю.
Уявіть інженерний розрахунок: 789/20 стає 39 9/20, допомагаючи точно спроектувати деталі. Такі приклади, з реальних сценаріїв, підкреслюють універсальність методу, роблячи його невід’ємним у професійних сферах.
Математична теорія за перетворенням
За лаштунками перетворення лежить основна властивість дробів: будь-який неправильний дріб можна виразити як суму цілого і правильного дробу. Формула проста – a/b = (q) + r/b, де q – частка, r – остача. Це корениться в евклідовому алгоритмі ділення, який використовується тисячоліттями, від античних математиків до сучасних комп’ютерних програм.
У глибині, це пов’язано з модульною арифметикою, де остача завжди менша за дільник, забезпечуючи правильність дробової частини. Для десяткових дробів перетворення подібне, але з акцентом на місце після коми – наприклад, 3.75 як неправильний дріб 15/4 стає 3 3/4. Така теорія додає глибини, показуючи, як прості операції будують складні системи.
Емоційно, розуміння цієї теорії ніби відкриває скриню скарбів, де кожне число має свою історію. Воно робить математику не сухою, а живою наукою, пов’язаною з еволюцією людського мислення.
Інструменти та онлайн-ресурси для перетворення
Сучасні калькулятори, як ті на освітніх сайтах, автоматизують процес, вводячи дріб і отримуючи мішане число миттєво. Наприклад, інструмент на ua.onlinemschool.com дозволяє перевірити розрахунки, додаючи впевненості новачкам. Ці ресурси, оновлені станом на 2025 рік, включають вправи для практики, роблячи навчання інтерактивним.
Мобільні додатки, такі як математичні помічники, пропонують крокові пояснення, ніби особистий tutor у кишені. Вони корисні для студентів, дозволяючи експериментувати з різними дробами без паперу. Однак, ручне перетворення розвиває глибше розуміння, тож поєднуйте інструменти з практикою для найкращого ефекту.
| Інструмент | Опис | Переваги |
|---|---|---|
| Онлайн-калькулятор | Автоматичне перетворення дробів | Швидкість і точність для перевірки |
| Мобільний додаток | Крокові інструкції з прикладами | Доступність у будь-який час |
| Шкільні вправи | Мануальні розрахунки з поясненнями | Розвиток навичок розуміння |
Ця таблиця ілюструє різноманітність інструментів, кожен з яких додає свій шар зручності. За даними домену ua.onlinemschool.com, такі ресурси допомагають мільйонам користувачів щороку, роблячи математику доступною.
Зворотне перетворення: з мішаного числа назад у неправильний дріб
Щоб повернутися, помножте цілу частину на знаменник і додайте чисельник – для 4 2/5 це (4 × 5) + 2 = 22/5. Цей процес, ніби дзеркальне відображення, підкреслює взаємозв’язок форм, дозволяючи гнучко маніпулювати числами в рівняннях.
У задачах з додаванням дробів зворотне перетворення спрощує операції, роблячи множення чи ділення легшим. Воно додає гнучкості, ніби дає ключі до різних дверей у математичному лабіринті. Практикуючи обидва напрямки, ви стаєте майстром дробів, здатним на складні розрахунки з легкістю.
Типові помилки при перетворенні
- 🚫 Ігнорування остачі: багато хто забуває відняти помножену частку від чисельника, отримуючи неправильний залишок – наприклад, для 10/3 виходить 3 1/3, але якщо пропустити, може вийти просто 3.
- 🚫 Плутанина зі знаками: для від’ємних дробів, як -8/5, знак ставиться перед цілою частиною (-1 3/5), а не розподіляється, що призводить до помилок у розрахунках.
- 🚫 Неправильне ділення: новачки ділять знаменник на чисельник, перевертаючи все догори дном – пам’ятайте, завжди чисельник на знаменник для частки.
- 🚫 Забуття скорочення: після перетворення дріб 4/8 у мішаному числі слід скоротити до 1/2, інакше форма залишається громіздкою.
- 🚫 Ігнор нульової остачі: якщо остача 0, як у 12/3 = 4, не додавайте нульовий дріб – це спрощує, але деякі додають зайве.
Ці помилки, ніби підводні камені в річці, можуть збити з пантелику, але усвідомлення їх робить процес безпечнішим. Уникаючи їх, ви перетворюєте навчання на впевнений шлях до майстерності.
Історія та еволюція дробів у математиці
Дроби з’явилися в Стародавньому Єгипті близько 1800 року до н.е., де неправильні форми перетворювали для вимірювання землі, як описано в папірусі Ахмеса. Греки, такі як Евклід, удосконалили теорію, вводячи алгоритми ділення, що лягли в основу сучасних методів. У середньовіччі арабські математики, як Аль-Хорезмі, поширили ці ідеї, роблячи перетворення частиною алгебри.
Сьогодні, у 2025 році, з розвитком комп’ютерів, перетворення автоматизоване, але розуміння історії додає шар поваги до цих простих операцій. Воно показує, як дроби еволюціонували від інструментів виживання до основ цифрової ери, надихаючи на глибше вивчення.
Практичні вправи для закріплення навичок
Спробуйте перетворити 15/4: ділення дає 3 з остачею 3, тож 3 3/4 – перевірте, додавши назад. Інша вправа: 22/7 ≈ 3 1/7, класичне наближення пі, показує зв’язок з геометрією. Для складнішого: 100/9 = 11 1/9, де велика остача вимагає точності.
Ці вправи, ніби тренування в спортзалі, зміцнюють розуміння, дозволяючи бачити патерни в числах. Регулярна практика перетворює теорію на інстинкт, роблячи вас впевненим у будь-яких математичних викликах.
Вправи з відповідями для самоперевірки
- 8/3: 2 2/3 – бо 3 × 2 = 6, 8 – 6 = 2.
- 19/5: 3 4/5 – перевірте множенням.
- 31/10: 3 1/10 – ідеально для десяткових вимірів.
Використовуючи ці приклади, ви не тільки закріплюєте навички, але й відкриваєте радість відкриття в математиці, де кожне перетворення – маленька перемога.
Застосування в шкільній програмі та за її межами
У шкільній програмі перетворення вводиться в 5-6 класах, допомагаючи учням переходити від простих дробів до складних операцій, як додавання чи множення. Воно формує основу для алгебри, де мішані числа спрощують рівняння. Поза школою, в професіях як архітектура чи програмування, цей навик економить час, роблячи розрахунки ефективними.
Наприклад, у програмуванні алгоритми ділення використовують для обробки даних, перетворюючи дроби в мішані для користувацьких інтерфейсів. Це показує, як базова математика переплітається з сучасними технологіями, додаючи практичної цінності знанням.
Найважливіше в перетворенні – не просто механіка, а розуміння, як воно робить числа частиною нашого світу, повного вимірів і пропорцій.
Розвиваючи цей навик, ви відкриваєте двері до безлічі можливостей, де математика стає союзником, а не перешкодою. З кожним новим дробом процес стає все природнішим, ніби розмова з давнім другом.