Рівнобедрений трикутник завжди зачаровує своєю симетрією, ніби дві рівні сторони обіймають основу, створюючи ідеальну гармонію форм. Ця фігура, з її рівними боками і часто несподіваними властивостями, стає ключем до багатьох геометричних загадок, від шкільних задач до реальних проєктів в архітектурі. А висота в такому трикутнику – це не просто лінія, а справжній місток між теорією і практикою, що розкриває секрети площі, кутів і навіть стійкості конструкцій.
Коли ви проводите висоту з вершини до основи, вона розбиває трикутник на два однакових прямокутних побратима, відкриваючи шлях до простих обчислень. Цей процес, насичений математичною елегантністю, дозволяє не тільки знайти числове значення, але й зрозуміти, як геометрія пульсує в повсякденному житті. Далі ми зануримося в деталі, розбираючи кожен крок з прикладами, що оживають на папері чи екрані.
Що Таке Рівнобедрений Трикутник і Чому Висота Важлива
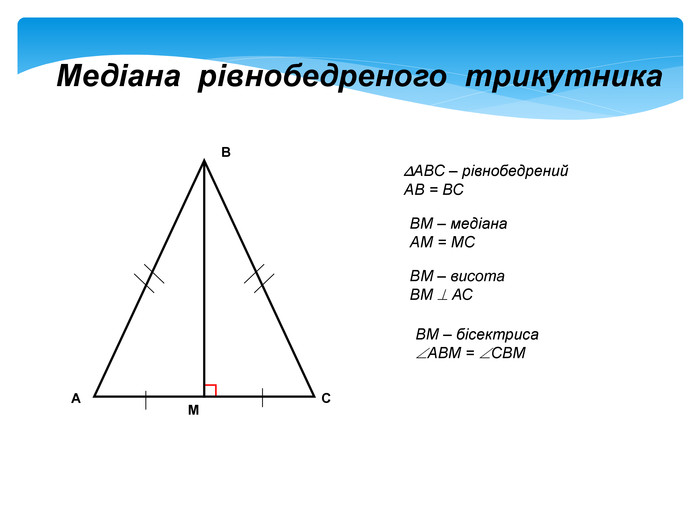
Рівнобедрений трикутник вирізняється двома рівними сторонами, які називаються бічними, і третьою – основою, що може бути довшою чи коротшою. Ця симетрія робить його улюбленцем у світі геометрії, де кути при основі завжди рівні, а вершинний кут додає характеру фігурі. Висота, проведена до основи, не просто вимірює відстань – вона стає інструментом для розрахунку площі, медіани чи навіть бісектриси, адже в такому трикутнику ці лінії часто збігаються.
Уявіть дах старовинного будинку, де рівнобедрений трикутник формує фронтон: висота тут визначає, наскільки стійкою буде конструкція під вагою снігу. Або ж у дизайні мостів, де точний розрахунок висоти запобігає колапсу. Ця величина, здавалося б проста, впливає на інженерію, мистецтво і навіть спорт, наприклад, у траєкторіях стрибків у воду, де геометрія тіла імітує трикутні форми.
За даними сайту mathros.net.ua, висота в рівнобедреному трикутнику завжди перпендикулярна основі і ділить її навпіл, створюючи два рівних сегменти. Це не просто правило – це фундамент, на якому будуються всі подальші розрахунки, роблячи фігуру передбачуваною і водночас захопливою.
Основна Формула для Обчислення Висоти
Серце розрахунку висоти б’ється в ритмі теореми Піфагора, яка оживає в половині трикутника. Якщо позначити рівні сторони як “a”, а основу як “b”, то висота “h” виражається формулою h = √(a² – (b/2)²). Ця елегантна рівність перетворює абстрактні числа на реальну довжину, ніби розкриваючи приховану енергію фігури.
Припустимо, у вас трикутник з бічними сторонами по 5 см і основою 6 см. Спочатку ділимо основу навпіл: 6/2 = 3 см. Потім підставляємо в формулу: h = √(25 – 9) = √16 = 4 см. Цей результат не тільки точний, але й наочно демонструє, як симетрія спрощує математику, роблячи її доступною навіть для новачків.
Але формула не стоїть на місці – вона адаптується. Якщо відомі кути, висоту можна знайти через тригонометрію: h = a * sin(α), де α – кут при вершині. Це додає гнучкості, дозволяючи обчислювати висоту в ситуаціях, коли прямі виміри недоступні, наприклад, у астрономічних спостереженнях за зірками, що утворюють трикутні конфігурації.
Варіанти Формул Залежно від Відомих Даних
Коли основа невідома, але є площа S, висота виходить з формули h = (2S)/b, де b – основа. Це перевертає перспективу, роблячи висоту похідною від загальної площі, ніби трикутник сам розповідає свою історію через числа.
Ще один підхід – через радіус вписаного чи описаного кола. Для вписаного: h = (3r * периметр) / (2 * основа), але це рідше використовується. Кожен варіант додає шар глибини, перетворюючи просту задачу на мозаїку можливостей.
Методи Обчислення: Від Простих до Складних
Найпростіший метод – геометричний: намалюйте трикутник, проведіть висоту і скористайтеся лінійкою для виміру. Але в реальності, коли фігура масштабна, як у проєктуванні пірамід, доводиться вдаватися до координатної геометрії. Розмістіть основу на осі X від (0,0) до (b,0), вершину на (b/2, h), і розрахунок стає візуальним шедевром.
Для складніших випадків, коли трикутник вписаний у коло, висота обчислюється через радіус R: h = (3/2) * √( (2R)^2 – b^2 / 4 ), але це вимагає знання радіуса. Такий підхід, натхненний античними математиками, додає історичного шарму сучасним розрахункам.
А в програмному забезпеченні, як GeoGebra, висоту можна знайти одним кліком, але розуміння ручних методів робить вас справжнім майстром, здатним розв’язати задачу навіть без гаджетів.
Покроковий Алгоритм для Початківців
Почніть з ідентифікації сторін: визначте, які дві рівні. Потім розділіть основу навпіл, утворивши прямокутний трикутник. Застосуйте Піфагора – і вуаля, висота готова. Цей алгоритм, простий як дитяча гра, ховає в собі потужність, що застосовується в усьому, від шкільних зошитів до інженерних креслень.
- Виміряйте рівні сторони (a) і основу (b).
- Розділіть основу на дві частини: b/2.
- Застосуйте формулу h = √(a² – (b/2)²).
- Перевірте результат, підставивши в площу: S = (b * h)/2.
- Якщо є кути, скористайтеся sin або cos для альтернативного розрахунку.
Ці кроки не просто інструкція – вони шлях до впевненості, де кожна дія наближає до відкриття. Після списку варто потренуватися на реальних прикладах, аби формули стали частиною вашого мислення.
Приклади з Реального Життя та Розрахунки
Уявіть рівнобедрений трикутник у формі намету: бічні сторони 4 м, основа 3 м. Висота h = √(16 – 2.25) = √13.75 ≈ 3.71 м. Це визначає, скільки місця всередині, роблячи геометрію практичною для кемпінгу чи фестивалів.
Інший приклад – у архітектурі, як у проєкті даху з кутами 45°. Якщо сторони 10 м, основа розраховується через косинуси, але висота виходить безпосередньо, забезпечуючи стійкість. А в спорті, наприклад, у фігурному катанні, траєкторія стрибка імітує висоту трикутника, де точність розрахунку запобігає травмам.
За даними сайту pochemychki.com.ua, такі приклади часто ігнорують новачки, але вони оживають, коли ви застосовуєте їх до щоденних задач, як вимірювання тіні від дерева, що формує трикутник із землею.
| Приклад | Сторони (a) | Основа (b) | Висота (h) | Застосування |
|---|---|---|---|---|
| Намет | 4 м | 3 м | ≈3.71 м | Кемпінг |
| Дах будинку | 10 м | 8 м | ≈8.72 м | Архітектура |
| Тінь дерева | 5 м | 4 м | ≈4.33 м | Вимірювання |
Ця таблиця ілюструє різноманітність, показуючи, як висота стає універсальним інструментом. Джерела даних: сайти myplanet.com.ua та mathros.net.ua.
Застосування в Сучасних Технологіях та Науці
У комп’ютерній графіці висота рівнобедреного трикутника моделює 3D-об’єкти, де алгоритми рендерингу розраховують тіні та перспективи з неймовірною точністю. У фізиці, при вивченні хвиль, така фігура описує амплітуду, а висота – пік енергії, роблячи математику живою силою.
Навіть у біології, форми листків чи крил комах часто нагадують рівнобедрені трикутники, де висота впливає на аеродинаміку. А в 2025 році, з розвитком AI, програми автоматично обчислюють висоту з фото, спрощуючи життя інженерам і дизайнерам.
Ці застосування перетворюють суху теорію на пульсуючу реальність, де кожен розрахунок – крок до інновацій.
Типові Помилки при Обчисленні Висоти
- 🚫 Не ділять основу навпіл: багато хто застосовує Піфагора безпосередньо до цілої основи, отримуючи помилкові результати, ніби ігноруючи симетрію фігури.
- 🚫 Плутанина з кутами: новачки часто беруть sin від кута при основі замість вершинного, що призводить до хаосу в розрахунках, наче переплутали ключі від дверей.
- 🚫 Ігнорування одиниць: забувають перевести см в м, роблячи висоту абсурдно великою чи малою, ніби вимірювали океан ложкою.
- 🚫 Неправильне округлення: в точних проєктах, як у будівництві, округлення до цілого може зруйнувати стійкість, підкреслюючи важливість точності.
- 🚫 Відсутність перевірки: без розрахунку площі для верифікації помилка ховається, як голка в стозі сіна, але проста перевірка рятує ситуацію.
Уникаючи цих пасток, ви перетворюєте геометрію на надійного союзника. А тепер, озброєні знаннями, ви готові до будь-яких трикутних викликів, де висота стає не бар’єром, а сходинкою до майстерності.