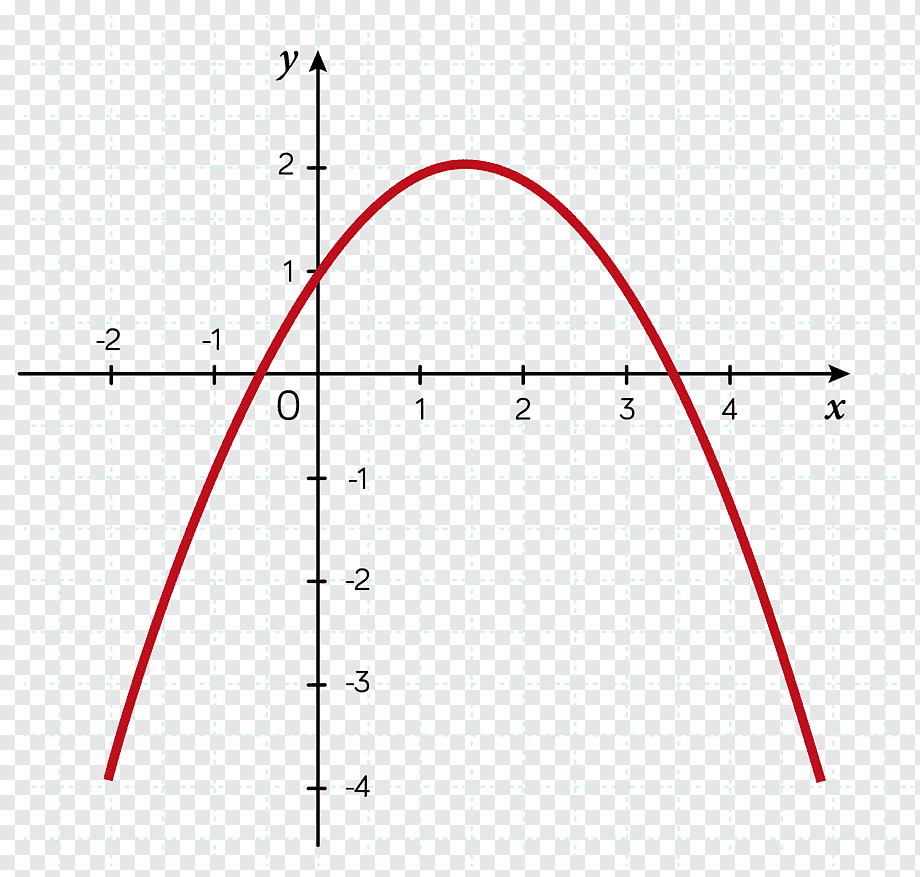
Корінь рівняння ховається в кожному математичному завданні, ніби та загадка, що чекає на розкриття. Візьміть просте рівняння 2x – 4 = 0. Якщо підставити x = 2, обидві сторони стають рівними: 0 = 0. Це класичний корінь – значення змінної, яке перетворює рівняння на істинну рівність. Таке базове поняття стає фундаментом для всього, від шкільних задач до моделювання ракетних траєкторій.
Але не поспішайте думати, що все так просто. Рівняння бувають хитрими: деякі мають кілька коренів, інші – жодного в реальних числах, а ще є ті, що ховають розв’язки в комплексному світі. Розуміння кореня відкриває двері до алгебри, фізики та програмування, де кожен корінь – ключ до реальних рішень.
Історія походження поняття: від глиняних табличок до сучасних комп’ютерів
Давні вавилоняни ще 4000 років тому ламали голову над квадратними рівняннями на глиняних табличках. Вони шукали корені для задач про площі полів чи об’єми зерен, використовуючи геометричні методи. Індійський математик Брахмагупта в VII столітті дав правила для квадратних рівнянь, а перс аль-Хорезмі заклав основи алгебри, де корінь став центральним поняттям.
Символ √ з’явився лише в 1525 році завдяки Крістофу Рудольфу – німецькому математику, який спростив позначення. У XVII столітті Декарт пов’язав рівняння з координатами, а Гаус довів фундаментальну теорему алгебри: кожен поліном n-го степеня має рівно n коренів у комплексних числах, рахуючи кратність. Ця еволюція перетворила корінь з архаїчного інструменту на потужну зброю науки.
Сьогодні чисельні методи, як метод Ньютона, дозволяють комп’ютерам знаходити корені з точністю до 10^{-15}, що критично для штучного інтелекту та квантових обчислень.
Точне визначення кореня рівняння та базові приклади
Формально, для рівняння виду f(x) = 0 коренем називають x_0 таке, що f(x_0) = 0. Це значення робить функцію нульовою, ніби точка дотику осі абсцис до графіка. Згідно з визначенням з uk.wikipedia.org, аргументи функцій рівняння, що задовольняють рівність, – корені.
Розгляньте лінійне рівняння 3x + 6 = 12. Віднімаємо 6: 3x = 6, ділимо на 3 – x = 2. Перевірка: 3*2 + 6 = 12. Ідеально. Тепер квадратне: x² – 5x + 6 = 0. Факторизуємо: (x-2)(x-3)=0, корені x=2, x=3.
Таблиця нижче порівнює прості типи рівнянь. Вона показує, скільки коренів очікувати та як їх шукати.
| Тип рівняння | Загальний вигляд | Кількість дійсних коренів | Формула коренів |
|---|---|---|---|
| Лінійне | ax + b = 0 | 1 | x = -b/a |
| Квадратне повне | ax² + bx + c = 0 | 0, 1 або 2 | x = [-b ± √(b²-4ac)] / (2a) |
| Кубічне | ax³ + bx² + cx + d = 0 | 1 або 3 | Кардано формула (складна) |
Дані таблиці базуються на стандартних алгебраїчних формулах (mathworld.wolfram.com). Після такої структуризації бачите: лінійні – найпростіші, квадратичні вже вимагають дискримінанта D = b² – 4ac для вибору шляху.
Множинність коренів та сторонні розв’язки
Один корінь – рідкість. Більшість рівнянь ховає кілька “скарбів”. Кратність кореня – скільки разів він повторюється, як у (x-1)²=0, де x=1 кратності 2. Графік торкається осі, не перетинаючи.
Сторонні корені з’являються при перетвореннях, наприклад, при √(x+1) = x-1. Квадратуємо: x+1 = (x-1)², отримуємо x=2 та x=0. Але x=0 не задовольняє оригінал (√1=0? Ні!). Завжди перевіряйте підставленням – це рятує від фальшивих надій.
У трансцендентних рівняннях, як sin(x) = 0.5, коренів безліч: x = π/6 + 2kπ. Область визначення (ОДЗ) звужує пошук.
Методи знаходження коренів: від аналітичних до чисельних
Аналітичні методи блискучі для поліномів до 4 степеня. Для квадратних – формула з дискримінантом. Якщо D>0 – два корені, D=0 – один, D<0 – комплексні.
Для вищих степенів звертаємося до чисельних. Метод бісекції ріже інтервал навпіл, де знак функції змінюється, гарантуючи збіжність. Метод Ньютона використовує похідну: x_{n+1} = x_n – f(x_n)/f'(x_n) – швидкий, але чутливий до стартової точки.
Ось кроки для методу хибного положення:
- Знайдіть інтервал [a,b], де f(a)*f(b) < 0.
- Обчисліть c = (a*f(b) – b*f(a)) / (f(b) – f(a)).
- Якщо f(c)=0 – готово. Інакше, замість знаку нульової сторони скоротіть інтервал.
- Повторюйте до бажаної точності.
Цей метод стабільний, ідеальний для комп’ютерів. У Python бібліотека SciPy має fsolve для автоматизації.
Графічний підхід: коли очі бачать краще формул
Графік f(x) перетинає вісь x у коренях. Для sin(x)=0 бачимо хвилі з точками на 0, π, 2π. Програми як Desmos чи GeoGebra візуалізують, допомагаючи підрахувати корені.
У реальності це рятує: інженери моделюють балки, шукаючи nuli напруг. Графіка показує множинність без розрахунків.
Типові помилки при пошуку коренів рівнянь
Забуваєте ОДЗ: у log(x)=0 x>0, інакше – помилка. Завжди перевіряйте!
- Не перевіряєте сторонні корені після піднесення до степеня – 30% помилок на тестах.
- Помилка в знаку дискримінанта: забуваєте 4ac.
- Ігноруєте кратність: (x-1)^3=0 має потрійний корінь.
- Стартова точка для Ньютона погана – розбігається.
Ці пастки ловлять навіть профі. Практикуйте перевірку – і корені стануть вашими друзями.
Комплексні корені: невидима сторона математики
Коли D<0 у квадратному, корені i√|D| – уявні. Але Гаус довів: у комплексах коренів рівно n. Наприклад, x² + 1 = 0 має x=±i. Вони правлять у квантовій механіці, електротехніці (AC-струми).
Розклад полінома на множники (x – r_k) веде до всіх коренів. Формула В’єта пов’язує суму коренів з коефіцієнтами – потужний інструмент.
Застосування коренів рівнянь у реальному світі
У фізиці: траєкторія снаряда – квадратне рівняння, корені дають часи польоту. Економіка: точка беззбитковості (TR – VC = FC) лінійне. У біології моделі популяцій Лотки-Вольтерри – нелінійні, корені показують рівноваги.
У 2025 році машинне навчання оптимізує нейромережі градієнтним спуском – по суті, Ньютона для багатовимірних. GPS розраховує позицію розв’язком нелінійних систем. Навіть у грі Fortnite фізика куль базується на коренях.
Кожен смартфон ховає мільйони таких обчислень. Розуміння коренів перетворює абстракцію на інструмент змін.
Ці приклади показують: корінь рівняння – не суха теорія, а жива сила, що рухає світом. Занурюйтесь глибше, і математика засяє новими барвами.