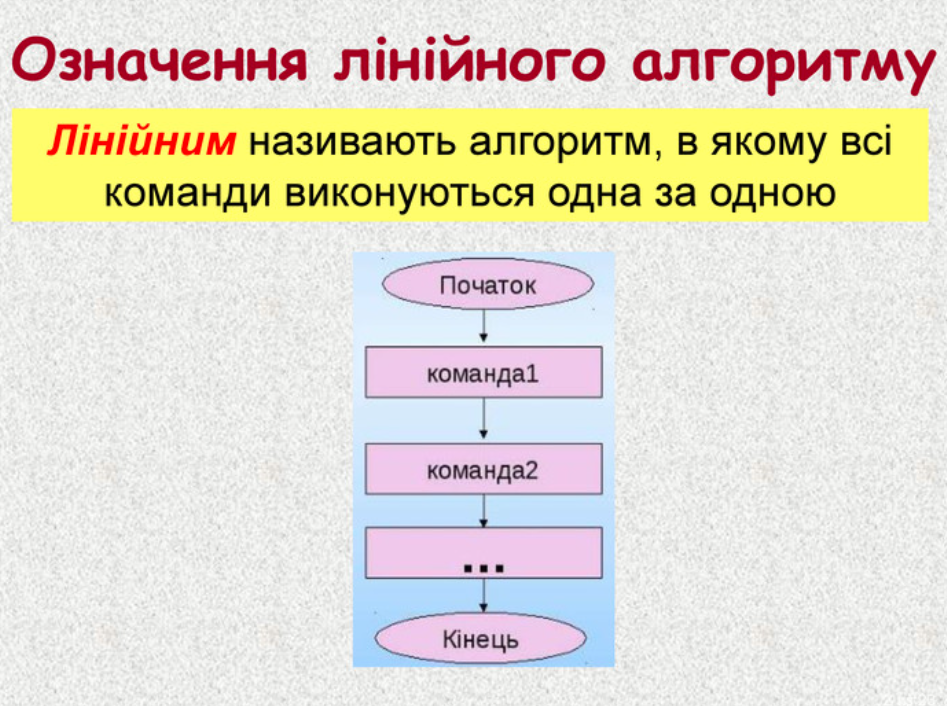
Лінійний алгоритм нагадує пряму стежку в густому лісі, де кожен крок веде точно до мети без зайвих поворотів чи петель. Це найпростіша форма алгоритму, де команди виконуються послідовно, одна за одною, без розгалужень на умови чи повторень у циклах. Кожна дія обов’язкова, і програма проходить весь шлях від початку до кінця рівно один раз. Уявіть рецепт ідеального борщу: нарізати буряк, варити бульйон, додати сметану — все строго по порядку, і страва виходить досконалою.
У програмуванні такий підхід ідеальний для простих обчислень, як знаходження суми чисел чи обчислення площі. Наприклад, щоб порахувати площу стін кімнати, вводимо довжину, ширину, висоту, множимо за формулою і виводимо результат — жодних “якщо” чи “повторити”. Ця структура лежить в основі багатьох початкових програм, від шкільних завдань до реальних скриптів. А тепер розберемося, чому це фундамент для всього складнішого.
Такий алгоритм не просто базовий інструмент — він вчить мислити послідовно, розкладати хаос на кроки. У світі, де програми обробляють мільйони даних, лінійні алгоритми часто стають основою для швидких рішень, особливо коли час на вагу золота.
Визначення та ключові характеристики лінійного алгоритму
Лінійний алгоритм будується на структурі слідування: команди йдуть ланцюжком, де кінець однієї зливається з початком наступної. Ніяких виборів, як у розгалужених алгоритмах з if-else, і ніяких петель, як у циклічних. Кількість операцій фіксована і дорівнює кількості рядків коду — це робить його передбачуваним, як тікання годинника.
Основні риси спалахують яскраво: повна детермінованість, відсутність залежності від умов, простота налагодження. Якщо щось йде не так, помилка ховається рівно там, де ви її написали. У шкільних підручниках це перша сходинка, бо вчить базовому алгоритмічному мисленню. Але в реальності лінійні алгоритми проникають скрізь — від мікроконтролерів у пральних машинах до скриптів обробки логів.
- Послідовність: Кожна команда виконується рівно один раз, у заданому порядку. Порушення — і алгоритм ламається.
- Відсутність розгалужень: Немає умовних переходів; все йде прямо.
- Фіксована довжина: Час виконання не залежить від вхідних даних у сенсі циклів — тільки від їхнього розміру для обчислень.
- Простота: Легко візуалізувати як пряму лінію в блок-схемі.
Після такого списку стає зрозуміло: лінійний алгоритм — це скелет будь-якої програми. Він не гнучкий, зате надійний, як старовинний міст через річку, що витримує бурі роками.
Історія розвитку поняття лінійного алгоритму
Корені сягають 1966 року, коли італійські вчені Коррадо Бем і Джузеппе Якопіні опублікували теорему структурованого програмування. Вони довели: будь-який алгоритм можна побудувати з трьох базових блоків — послідовності (лінійний), розгалуження та циклу. Лінійний блок став фундаментом, бо без нього немає основи для складніших конструкцій. До того програмування тонуло в спагеті-коді — хаосі goto-стрибків, де відстежити логіку було мукою.
Ця теорема перевернула індустрію: мови на кшталт Pascal, C, Python увібрали ідею структури. У 1970-х лінійні алгоритми стали стандартом у навчанні, а в 2020-х вони еволюціонували в мікросервіси, де прості скрипти обробляють дані в реальному часі. Сьогодні, у 2026-му, з ростом edge computing, лінійні алгоритми повертаються тріумфом у IoT-пристроях, де кожна мілісекунда на рахунку.
Історичний поворот надихає: з простої лінії виросла вся сучасна інформатика. Без Бема-Якопіні не було б чистого коду в GitHub мільйонах репозиторіїв.
Структура лінійного алгоритму: від блок-схем до псевдокоду
Блок-схема лінійного алгоритму — це ланцюг прямокутників, з’єднаних стрілками вниз. Початок (овал), ввід даних, обробка, вивід, кінець. Простіше пареної картоплі! Наприклад, для обчислення площі трикутника: ввід a, b, c; периметр p = (a+b+c)/2; площа S = sqrt(p*(p-a)*(p-b)*(p-c)); вивід S.
Псевдокод робить це універсальним:
- Початок
- a ← ввід(“сторона a”)
- b ← ввід(“сторона b”)
- c ← ввід(“сторона c”)
- p ← (a + b + c) / 2
- S ← sqrt(p * (p – a) * (p – b) * (p – c))
- Вивід(“Площа: “, S)
- Кінець
Така структура гарантує, що програма не “зациклиться” чи не пропустить крок. У реальному коді це перекладається в будь-яку мову, додаючи лише синтаксис.
Приклади лінійного алгоритму в повсякденному житті та простих задачах
Щодня ми виконуємо лінійні алгоритми несвідомо: увімкнути кавоварку — налити воду, засипати зерна, натиснути старт. Або зарядити телефон: вставити кабель, підключити до розетки, чекати індикатора. Ці послідовності — чиста лінійність, бо жоден крок не залежить від умов.
У математиці — обчислення відсотків: сума, ставка, термін; відсоток = сума * ставка * термін / 100; вивід. Шкільний приклад площі кімнати оживає: для кімнати 5x4x2.5 м площа стін 2*(5+4)*2.5 = 45 м². Просто і елегантно.
Гумор у тому, що якщо пропустити крок — кава без води, телефон не зарядиться. Так само в коді: без виводу результат зникає в нікуди.
Реалізація лінійних алгоритмів у сучасних мовах програмування
У Python лінійний алгоритм сяє простотою. Ось обчислення площі кімнати:
a = float(input("Довжина: "))
b = float(input("Ширина: "))
h = float(input("Висота: "))
s = 2 * (a + b) * h
print("Площа стін:", s)
Виконується рядок за рядком, блискавично. У JavaScript для веб-форми:
let a = parseFloat(prompt("Довжина:"));
let b = parseFloat(prompt("Ширина:"));
let h = parseFloat(prompt("Висота:"));
let s = 2 * (a + b) * h;
alert("Площа: " + s);
C++ додає типи для ефективності:
#include <iostream>
#include <iomanip>
int main() {
double a, b, h;
std::cin >> a >> b >> h;
double s = 2 * (a + b) * h;
std::cout << "Площа: " << std::fixed << std::setprecision(2) << s << std::endl;
return 0;
}
Кожна мова підкреслює: лінійність робить код читабельним, як відкриту книгу. У 2026-му Python домінує в data science для таких швидких обчислень.
Лінійна складність алгоритмів: O(n) як серце лінійності
Тут лінійний алгоритм набуває нового виміру: часова складність O(n), де n — розмір даних. Це означає, алгоритм виконує пропорційно n операцій. Класика — лінійний пошук елемента в масиві: проходимо від першого до останнього, порівнюємо. Найгірший випадок — O(n), середній — O(n/2).
Приклад у Python для суми масиву:
def sum_array(arr):
total = 0
for num in arr: # Лінійний прохід
total += num
return total
Хоч цикл виглядає як повтор, для фіксованого n це лінійне. У великих даних O(n) кращий за O(n²), бо масштабується лінійно. Insertion sort — ще один герой: вставляємо елементи по черзі, середня складність O(n²), але базові кроки лінійні.
| Алгоритм | Найкращий випадок | Середній | Найгірший |
|---|---|---|---|
| Лінійний пошук | O(1) | O(n/2) | O(n) |
| Сума масиву | O(n) | O(n) | O(n) |
| Бінарний пошук (для порівняння) | O(1) | O(log n) | O(log n) |
Джерела даних: uk.wikibooks.org, en.wikipedia.org (станом на 2026). Таблиця показує: лінійні виграють у простоті, але програють логарифмічним у великих n.
Переваги та недоліки лінійних алгоритмів
Переваги виблискують: легкість розуміння, мінімальний час розробки, нульовий ризик нескінченних циклів. Ідеально для прототипів чи вбудованих систем, де пам’ять обмежена. Недоліки кусаються: не гнучкі для складних задач, неефективні для великих даних без оптимізації.
- Швидка реалізація — код пишеться за хвилини.
- Легке тестування — кожен крок перевіряється окремо.
- Низьке споживання ресурсів — без зайвих структур.
У балансі лінійні — стартова ракета для будь-якого проекту. Додайте розгалуження — і отримайте повноцінну програму.
Практичні кейси лінійних алгоритмів
У логістиці: обробка черги клієнтів — ввід замовлення, розрахунок суми, друк чеку. У 2026-му це скрипт для POS-терміналів, що економить секунди на тисячі транзакцій.
Веб-скрейпінг: пройти по сторінці, витягти заголовки по черзі — простий парсер новин на JS. Кейс з реальним проектом: автоматизація звітів у Google Sheets API, де лінійний прохід по рядках генерує PDF щодня.
IoT: сенсор температури — зчитати значення, конвертувати в Цельсій, відправити на сервер. У смарт-термостатах це виконується за мілісекунди, без лагів.
Ці кейси доводять: лінійні алгоритми живуть у production, де надійність важливіша за фішки.
З таких прикладів видно, як простота переростає в потужність. Лінійний алгоритм не вмирає — він еволюціонує, проникаючи в нейромережі як препроцесинг даних чи в блокчейн для валідації транзакцій по черзі.
Ентузіазм переповнює: спробуйте самі написати лінійний скрипт для щоденних обчислень, і відчуєте магію послідовності. А для просунутих — комбінуйте з векторизацією в NumPy, де O(n) стає супершвидким на GPU.