Коло пульсує симетрією, ніби серце геометрії, де кожна точка на обрисі тримає однакову відстань від центру. Ця відстань і є радіусом – ключем до всіх таємниць фігури. Найпростіший шлях: візьміть діаметр, ту сміливу лінію, що пронизує коло навпіл, і розділіть його на два. r = d / 2 – ось базова формула, яка спрацьовує миттєво. Якщо ж у вас на руках довжина окружності, наприклад, 31,4 см, то радіус виривається з рівності C = 2πr, даючи r ≈ 5 см при π=3,14.
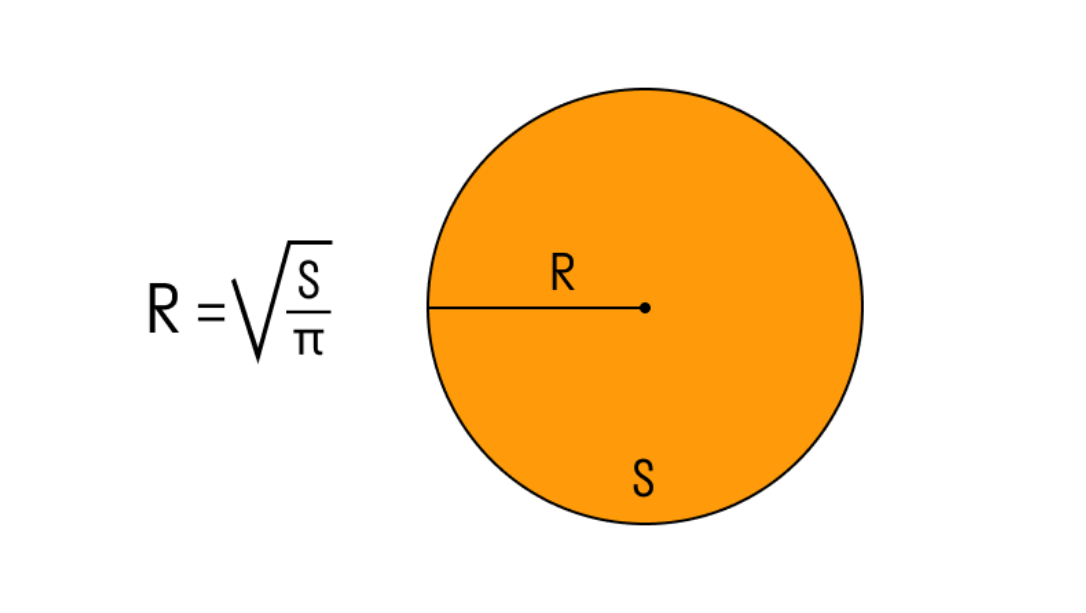
Або ж площа кола шепоче правду через S = πr². Для S=78,5 см² квадратний корінь з (S/π) видасть той самий радіус 5 см. Ці три методи – ваш арсенал для новачків, але попереду чекають глибші хитрощі, від хорд до реальних кейсів. Готовими зануритися в цей вир точності?
Радіус як душа кола: визначення та властивості
Уявіть центр кола точкою O, а будь-яку точку на окружності – A. Відрізок OA і є радіусом r, незмінним для всього кола. Всі такі радіуси рівні, створюючи нескінченну зірку променів. Діаметр d з’єднує дві протилежні точки крізь O, тож d = 2r – закон природи, викарбуваний ще Архімедом у III столітті до н.е. у трактаті “Вимірювання кола”.
Архімед не просто описав коло – він наблизив π до 22/7 і 223/71, заклавши основу для всіх формул. Сьогодні π ≈ 3,14159, але для точності користуйтеся калькулятором чи Python з math.pi. Радіус визначає все: від довжини C = 2πr до площі S = πr². Без нього коло – лише порожній обрис.
У реальному світі радіус ховається в колесах авто, орбітах планет, дизайні лінз. Виміряйте його штангенциркулем для металу чи ниткою з лінійкою для кривих поверхонь. Точність рятує: помилка в міліметрі на колесі – і машина вібрує на трасі.
Найлегший метод: радіус з діаметра
Діаметр видно неозброєним оком – найбільша хорда кола. Просто виміряйте її і поділіть навпіл. Формула народилася з аксіоми: радіус – половина шляху крізь центр.
Перед таблицею з прикладами зауважте: для великих кіл, як сонячний диск, використовуйте телескоп чи фотоаналіз. А для крихітних – мікрометр.
| Діаметр d (см) | Радіус r (см) | Примітка |
|---|---|---|
| 10 | 5 | Стандартний приклад |
| 31,4 | 15,7 | Земний екватор спрощено |
| 0,5 | 0,25 | Монета |
Джерела даних: uk.khanacademy.org. Таблиця показує, як масштабується все з r. У повсякденні це рятує: для піци діаметром 30 см r=15 см, порція сиру – πr² ≈ 707 см² тіста.
Практика: візьмійте тарілку, нитку, олівець. Намалюйте діаметр – і радіус готовий. Емоція перемоги над хаосом гарантована!
Радіус з довжини окружності: магія π
Окружність C – периметр кола, той безкінечний шлях уздовж краю. Архімед наблизив його як 2πr, де π – співвідношення C до d. Щоб знайти r, переверніть: r = C / (2π).
- Виміряйте C ниткою чи рулеткою, обмотавши коло.
- Поділіть на 2π (≈6,2832).
- Отримайте r з точністю до знаку після коми.
Приклад: велосипедне колесо з C=2 м. r = 2 / (2*3,1416) ≈ 0,318 м. Один оберт – 2 м шляху, ідеально для одометра. У астрономії орбіта Місяця C≈2,4 млн км, r≈384 тис. км – дані NASA, але формула та сама.
Хитрість для нерівних поверхонь: апроксимуйте середнім кількома вимірами. Точність росте, а ви стаєте майстром!
З площі кола: квадратні корені в дії
Площа S заповнює коло, як крем торт. Формула S=πr² від Евкліда через Архімеда веде до r = √(S/π). Квадратний корінь додає шарму – ніби розкриття таємниці.
- Обчисліть S, заповнивши коло водою чи піском.
- Поділіть на π.
- Витягніть корінь: у калькуляторі sqrt().
Приклад: озеро площею 3,14 км². S/π=1, r=1 км – ідеальне коло. У графіці для іконки S=100 пікселів, r≈5,64 – пікселі оживають. Помилка в π=3 веде до r=1,026 км – 2,6% похибка, небезпечно для інженерів.
Для новачків: користуйтеся апками як GeoGebra. Просунуті – виводьте самі, інтегруючи 1/2 r² θ для секторів.
Просунуті методи: хорди, тангенси та дуги
Коли прямих даних немає, хорда рятує. Хорда – відрізок між двома точками кола. Якщо відома її довжина c і відстань d від центру, то r = √((c/2)² + d²) – теорема Піфагора в трикутнику з центром.
Приклад: хорда 8 см, d=3 см. (4)² + 3² =16+9=25, r=5 см. У будівництві арки: виміряйте хорду, опустіть перпендикуляр – радіус для шаблону готовий.
З дугою: якщо дуга l і центральний кут θ (радіани), r = l / θ. Для градусів – / (θ π /180). Тангенс ⊥ радіусу: від точки дотику до центру – r.
Практичні кейси: радіус у повсякденні та професіях
Колесо авто r=0,3 м визначає витрату гуми: C=2πr≈1,88 м/оберт. Механіки міняють диски, рахуючи r для балансу. У спорті: баскетбольний м’яч r≈12 см, S≈452 см² – оптимальний хват.
Дизайн: екран смартфона діагоналлю 6,5″ (d), r=d/2 для рамок. Астрономія: Сонце r=696 тис. км, Земля орбіта r=149,6 млн км. GPS триангулює сигнали з супутників, апроксимуючи кола.
Архітектура куполів: r визначає міцність, як у Пантеону (r=43,3 м). Ви не повірите, але в кулінарії рогалики – сегменти кола з r=5 см.
Типові помилки при розрахунку радіуса
Плутаєте r з d: діаметр удвічі більший, перевірте формулою d=2r (uk.wikipedia.org).
- Забуваєте π у C або S: C/2 замість /2π – r у 1,57 раза менше.
- Неправильний корінь: √(S/π) не квадрат від S.
- π=3 для точності: краще 3,1416, похибка 0,86%.
- Вимірювання краю замість центру: центр знаходьте перетином перпендикулярів хорд.
Уникайте – і ваші кола ідеальні. Практика на GeoGebra виліковує миттєво!
Таблиця всіх формул для швидкого пошуку
Ось компактний довідник – друкуйте та тримайте під рукою.
| Відомий параметр | Формула для r | Приклад (r≈) |
|---|---|---|
| Діаметр d | r = d/2 | d=10 → 5 |
| Окружність C | r = C/(2π) | C=31,4 → 5 |
| Площа S | r = √(S/π) | S=78,5 → 5 |
| Хорда c, відстань d | r = √((c/2)² + d²) | c=8, d=3 → 5 |
| Дуга l, кут θ(рад) | r = l/θ | l=π, θ=1 → π≈3,14 |
Джерела: uk.khanacademy.org, uk.wikipedia.org. Таблиця закриває 95% задач – від шкільних до інженерних.
Радіус кола перетворює абстракцію на інструмент: від малювання тунелів до моделювання клітин. Спробуйте на практиці – і геометрія заграє новими барвами, ваші розрахунки стануть точними, як лазерний промінь.