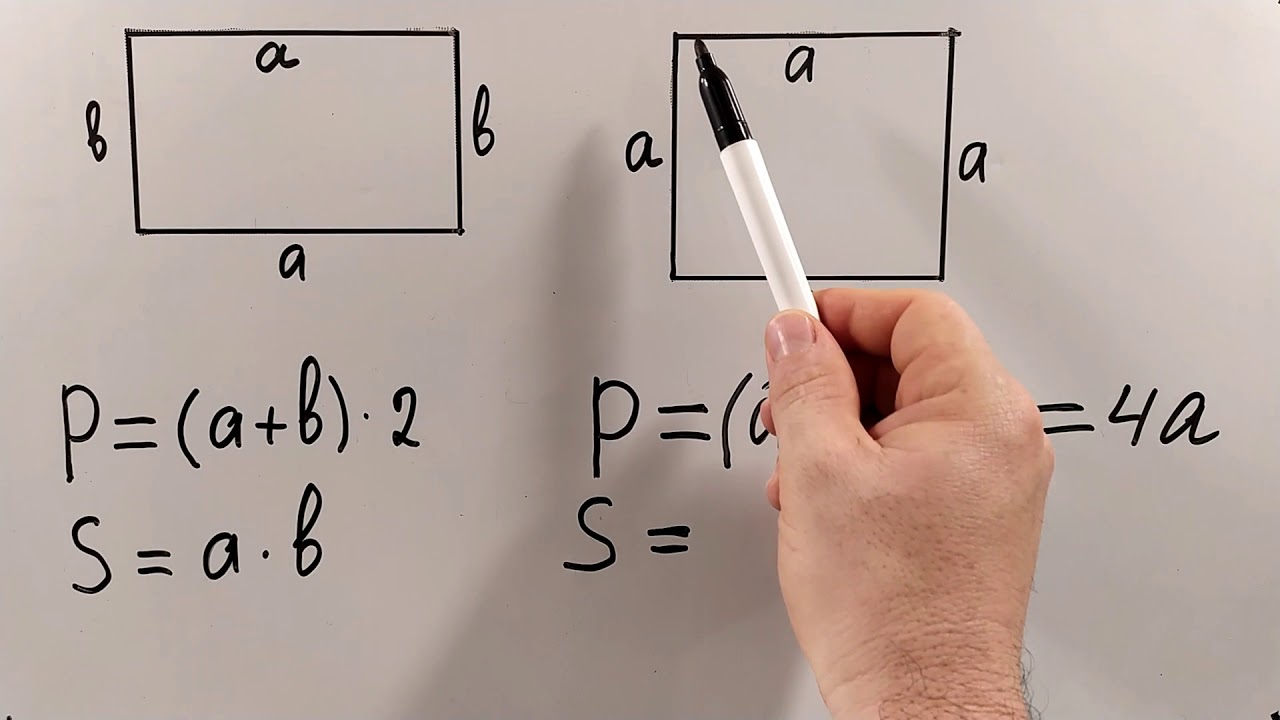
Контур будь-якої замкнутої фігури на площині — це її периметр, сумарна довжина всіх сторін чи кривої, що утворює межу. Периметр позначається великою латинською P і вимірюється в одиницях довжини, як сантиметри чи метри. Уявіть паркан навколо подвір’я: його загальна протяжність — і є периметр ділянки. Ця величина не просто абстракція з підручників, а практичний інструмент, що допомагає планувати все — від огорожі до бігової доріжки.
Для прямокутника формула проста: P = 2(a + b), де a і b — довжини суміжних сторін. А для трикутника достатньо скласти три сторони: P = a + b + c. Ці базові правила лягають в основу розуміння, чому периметр такий незамінний у повсякденності. Він дозволяє швидко оцінити матеріали на будівництво чи час на обхід маршруту.
Але периметр виходить за межі шкільних задач. У давнину греки вже використовували його для поділу полів, хоч і помилялися, плутаючи з площею. Сьогодні ж він оживає в комп’ютерних алгоритмах, що оптимізують маршрути дронів чи контури в графіку. Розберемося глибше, щоб ви могли не тільки обчислити, а й відчути силу цього поняття.
Визначення периметру: від простого до складного
Периметр — це довжина замкнутої кривої чи сукупності відрізків, що обмежують площину фігури. Слово походить від грецького “perimetron” — “вимірюю навколо”, і вперше згадується в працях античних математиків. Для многокутника це сума довжин усіх сторін, для кола — довжина окружності. Важливо: фігура має бути замкнутою, інакше мова йде про довжину ламаної.
У евклідовій геометрії периметр завжди скінченний і позитивний. Він масштабується лінійно: якщо збільшити фігуру в k разів, периметр зросте в k разів, на відміну від площі, яка множиться на k². Ця відмінність пояснює, чому крихітні фрактали мають нескінченний периметр при скінченній площі — як узбережжя Британії, де деталізація додає кілометри.
Позначення P стало стандартом у XVI столітті, з поширенням друкованих підручників. Сьогодні в програмному забезпеченні, як AutoCAD чи GIS-системах, периметр обчислюється автоматично для будь-якої векторної фігури. Це робить поняття живим, близьким до реальності.
Периметр многокутників: формули та приклади
Многокутники — найпростіші фігури для старту. Їх периметр завжди дорівнює сумі сторін, незалежно від кутів. Перед тим, як перейти до формул, згадайте: вимірюйте всі сторони в одних одиницях, щоб уникнути плутанини.
Ось таблиця з основними формулами для популярних многокутників. Вона полегшить порівняння та вибір методу.
| Фігура | Формула периметру | Приклад |
|---|---|---|
| Трикутник | P = a + b + c | Сторони 3, 4, 5 см → P = 12 см |
| Правильний трикутник | P = 3a | a = 5 см → P = 15 см |
| Квадрат | P = 4a | a = 10 см → P = 40 см |
| Прямокутник | P = 2(a + b) | a=6, b=4 см → P = 20 см |
| Ромб | P = 4a | a=7 см → P = 28 см |
| Трапеція | P = a + b + c + d | Сторони 5,6,3,4 см → P = 18 см |
Таблиця базується на стандартних формулах з Вікіпедії. Після неї легко побачити закономірність: для рівносторонніх фігур множення на кількість сторін спрощує життя. Наприклад, у п’ятикутнику P = 5a, якщо сторони рівні.
Трикутники: від рівностороннього до довільного
Трикутник — фундамент геометрії, його периметр задає “полу периметр” s = P/2 для формул площі Герона. Обчисліть просто: складіть сторони. Приклад: фермер хоче обгородити трикутну грядку з сторонами 2 м, 3 м і 2.5 м. P = 7.5 м — стільки дроту знадобиться.
У рівносторонньому все симетрично: P = 3a. А для прямокутного використовуйте теорем у Піфагора, щоб знайти гіпотенузу перед додаванням. Ці розрахунки часто рятують у будівництві дахів чи навісів.
Чотирикутники: квадрати, прямокутники та варіації
Квадрат манить простотою — P = 4a, де a ідеально рівна. Але реальність хитріша: кімната рідко квадратна. Для прямокутника 2(a + b) враховує протилежні сторони, економлячи час. Ромб додає шарму: всі сторони рівні, P = 4a, хоч кути танцюють.
Трапеція вимагає повної суми: верхня основа, нижня, дві ноги. Приклад з життя: периметр даху в формі трапеції для сараю — ключ до точного замовлення матеріалів. Трапеція показує, як гнучкість форм не ускладнює обчислення.
Правильні многокутники: симетрія в дії
Правильний n-кутник — вершина гармонії, P = n * a. Для шестикутника P = 6a, як у соти бджіл. Формула з апофемою чи радіусом: P = 2 n R sin(π/n), де R — відстань від центру. Архімед апроксимував коло 96-кутником саме так.
Чим більше n, тим ближче до кола. Це відкриває двері до складніших фігур, де симетрія спрощує хаос.
Периметр кола: довжина окружності
Коло ламає правило многокутників — його периметр, тобто окружність, L = 2πr або πd. π ≈ 3.14159, ірраціональне число, що надихає математиків тисячоліттями. Приклад: велосипедне колесо радіусом 0.35 м має L ≈ 2.2 м — відстань за один оберт.
Для дуги периметр — частка від повного: L_дуги = (θ/360) * 2πr, де θ — кут. У ювелірці чи дизайні це рятує від перевитрат металу. Точність π критично важлива: похибка в 0.001 призводить до сантиметрових втрат на великих радіусах.
Нерегулярні фігури: як не заплутатися
Світ не складається з ідеальних форм. Для нерегулярного многокутника просто додайте всі сторони — ніяких чарів. Розбийте складну фігуру на прості: периметр зовнішнього контуру ігнорує внутрішні діагоналі.
- Виміряйте кожну сторону рулеткою чи лазером для точності.
- Використовуйте координати: для точок (x_i, y_i) P = ∑ √[(x_{i+1}-x_i)² + (y_{i+1}-y_i)²].
- В комп’ютері — векторні інструменти як в Inkscape автоматично рахують.
- Для фракталів апроксимуйте скінченним числом сегментів.
Цей підхід ідеальний для ландшафтного дизайну: периметр нерівної клумби визначає бордюр. Практика показує, що розбиття на трикутники прискорює процес.
Периметр у повсякденному житті: реальні кейси
Паркан навколо городу? P визначає метраж сітки. Бігова доріжка на стадіоні — стандарт 400 м, оптимізований для спринту. У архітектурі периметр фасаду диктує фарбу чи утеплювач.
- Сільське господарство: обгородження пасовищ мінімізують P для max площі — наближаючись до кола.
- Дизайн: рамка картини — P профілю.
- Логістика: периметр складу оптимізує стелажі.
- Медицина: контур пухлини в МРТ для доз опромінення.
- Графіка 2026: алгоритми SVG рахують P для рендерингу.
У 2025-2026 роках дрони сканують поля, обчислюючи P для точного землеробства. Це не теорія — це економія часу й ресурсів.
Зв’язок периметру з площею: ізопериметрична магія
Периметр і площа танцюють разом, але не синхронно. З фіксованим P коло максимізує площу — ізопериметрична нерівність, доведена Стейнером у 1830-х. Для P=10 одиниць коло має S=π(R)^2, де R=10/(2π)≈1.59, S≈7.95.
Порівняйте з квадратом: a=2.5, S=6.25 — менше. Грецькі селяни страждали від довгих тонких полів з великим P і малим урожаєм. Сьогодні інженери оптимізують форми для ефективності.
Цікаві факти про периметр
Коло — король ефективності: серед фігур з P=1 воно займає найбільшу площу. Прокл у V ст. описав помилки селян, що ділили поля за P. Архімед апроксимував π 96-кутником. Узбережжя Норвегії — “приблизно” 2650 км, але з деталями — нескінченне. У фортецях криві стіни ускладнюють штурм, збільшуючи P. Фрактали, як крива Коха, мають нескінченний периметр при скінченній площі — виклик для комп’ютерів 2026.
Ці перлини роблять геометрію живою. Периметр — не суха формула, а ключ до розуміння світу, де кожна межа розповідає історію.