Дотична пряма торкається кривої в одній точці, немов легкий поцілунок вітру до поверхні озера, ідеально повторюючи її напрямок саме там, де це найважливіше. Уявіть коло: від зовнішньої точки проведіть дві лінії, які чіпляються за його край, не проникаючи всередину — це і є дотичні. Вони не перетинають коло, а лише дотикаються, утворюючи перпендикуляр з радіусом у точці контакту. Ця проста ідея лежить в основі геометрії, диференціального числення та навіть сучасних комп’ютерних симуляцій.
У аналітичній геометрії дотична до графіка функції y = f(x) у точці x₀ набуває форми y – f(x₀) = f'(x₀)(x – x₀), де f'(x₀) — похідна, що показує кут нахилу. Для початківців це означає: похідна не просто число, а живий нахил лінії, яка найкраще апроксимує криву. Просунуті читачі оцінять, як це узагальнюється на вищі порядки дотику чи многовиди.
Чому це круто? Бо дотична — місток між статичною геометрією та динамікою руху, дозволяючи моделювати швидкості, кривизну та наближення в реальному світі. Тепер зануримося глибше, розбираючи кожен шар цього поняття.
Геометричне розуміння дотичної
Коли Евклід у “Началах” згадував дотичну до кола, він уже інтуїтивно відчував її суть: пряма, яка межує з кривою, не перетинаючи її всередині. Сучасне визначення точніше — дотична збігається з кривою в точці з точністю до першого порядку, тобто їхні похідні рівні. Граничне положення січної, коли дві точки зближуються, дає цю лінію.
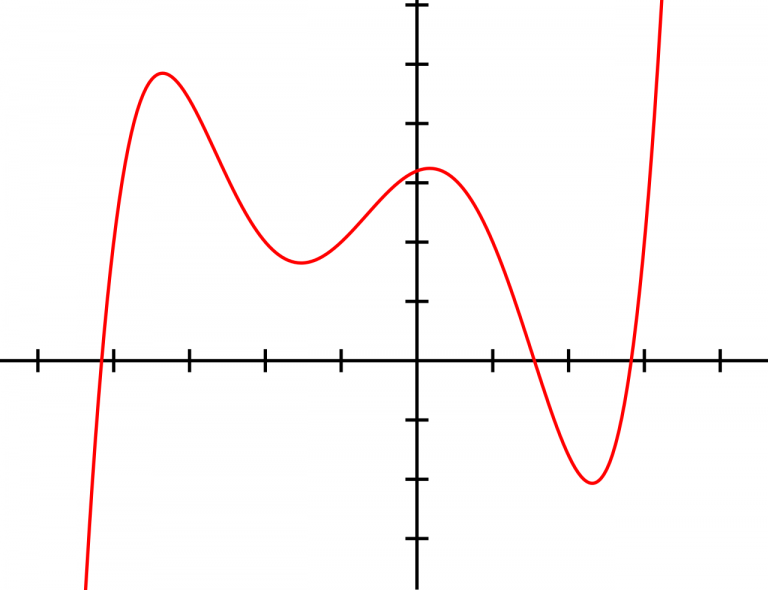
Уявіть параболу y = x²: у точці (1,1) січні з сусідніми точками все ближче повторюють нахил 2. Результат — дотична y = 2x – 1, що ковзає вздовж кривої, немов рука по гладкій поверхні. Це не магія, а математика, яка оживає на графіках.
Для новачків: візьміть олівець і обведіть коло — лінія, що торкається краю, не заходячи всередину, і є дотичною. Просунуті: у диференціальній геометрії дотичний вектор задає напрямок, утворюючи дотичний простір розмірності многовиду.
Історія: від античності до диференціального числення
Архімед ще 2000 років тому малював дотичну до спіралі, розглядаючи рух точки. Аполлоній Пергський у “Конічних перетинах” визначив її як межу, де між прямою і кривою не влізе жодна інша. У 1630-х П’єр Ферма винайшов метод максимумів, обчислюючи дотичні через малі прирости — прообраз похідної.
Рене Декарт удосконалив це методом нормалей, а Жиль Роберваль бачив криві як композицію простіших рухів. Кульмінація — XVII століття: Ньютон і Лейбніц формалізували, перетворивши дотичну на інструмент аналізу. До 1828 року визначення еволюціонувало від “не перетинає” до сучасного, що дозволяє точки перегину.
Ці відкриття не просто теорія — вони революціонізували фізику Ньютона, де дотична траєкторії дає миттєву швидкість. Сьогодні ми стоїмо на плечах гігантів, і дотична пульсує в кожному алгоритмі машинного навчання.
Дотична до кола: властивості та теореми
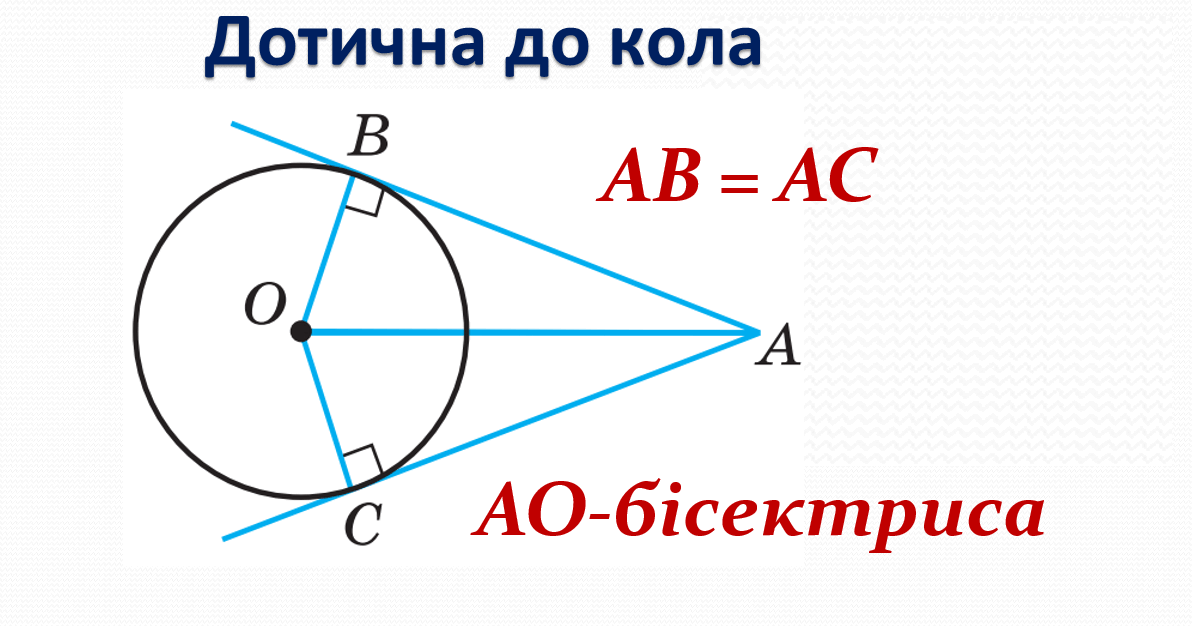
До кола з центром O і радіусом R дотична в точці T перпендикулярна OT. Це фундамент: довжину дотичної з зовнішньої точки P обчислюють як √(PT² = PO² – R²). З P ведуть дві дотичні, рівні за довжиною.
Теорема про січну: PT² = PB · PC, де AB — січна з P через B і C на колі. Кут між дотичною і хордою дорівнює куту в напівколі. Для двох кіл — зовнішні та внутрішні дотичні, центри гомотетії визначають їх перетин.
- Зовнішня дотична: не проходить між колами, довжина L = √(d² – (R1 – R2)²), де d — відстань центрів.
- Внутрішня: перетинає, L = √(d² – (R1 + R2)²) для перекритих.
- Теорема Монже: для трьох кіл шість дотичних, центри на прямих гомотетії.
Після побудови допоміжних кіл для зовнішніх/внутрішніх, дотичні оживають у задачах Аполлонія чи більярді, де кулі “стрибають” по дотичним.
Дотична до графіка функції: роль похідної
Похідна f'(x₀) — тангенс кута нахилу дотичної. Для y = sin(x) у x=0 похідна cos(0)=1, дотична y = x — горизонтальний дотик стає похилим. У точках максимуму/мінімуму f'(x)=0, дотична горизонтальна.
Приклад: y = x³ – 3x у x=1, f'(x)=3x²-3=0? Ні, f'(1)=0, точка перегину з горизонтальною дотичною y=-2. Крива перетинає дотичну, але збігається по похідній.
- Обчисліть f(a) — координата точки.
- Знайдіть f'(a) — нахил.
- Запишіть y – f(a) = f'(a)(x – a).
- Перевірте: підставте сусідні точки, похибка мала.
Цей алгоритм — основа CAD-систем, де моделі “торкаються” ідеально.
Рівняння дотичної для різних кривих
Перед таблицею: для конічних перетинів існують стандартні формули, що спрощують обчислення без похідних. Ось порівняння для класичних кривих у точці (x₀, y₀).
| Крива | Рівняння дотичної |
|---|---|
| Коло (x-a)² + (y-b)² = R² | (x₀-a)(x-a) + (y₀-b)(y-b) = R² |
| Парабола y² = 4ax | yy₀ = 2a(x + x₀) |
| Еліпс x²/a² + y²/b² = 1 | (x x₀)/a² + (y y₀)/b² = 1 |
| Гіпербола x²/a² – y²/b² = 1 | (x x₀)/a² – (y y₀)/b² = 1 |
Джерела даних: uk.wikipedia.org (розділ “Дотична”). mathros.net.ua.
Для параметричних кривих x(t), y(t): нахил dy/dx = y'(t)/x'(t), рівняння через t₀. Неявні: F(x,y)=0, градієнт ∇F перпендикулярний дотичній.
Нормаль: перпендикулярний супутник
Нормаль — лінія, перпендикулярна дотичній у точці дотику. Нахил -1/f'(x₀). У фізиці нормаль задає напрямок сили опору. Для кола — це радіус, просте і елегантне.
Приклад: до y=x² у (1,1), дотична нахил 2, нормаль -1/2, рівняння y-1 = -0.5(x-1). Вони танцюють удвох, утворюючи гармонію площини.
Дотичні у просторі: лінії та площини
Для просторової кривої r(t)=(x(t),y(t),z(t)) дотична — r(t₀) + r'(t₀)t. Нормаль і бінормаль з тригранника Френе додають кривизну. Дотична площина до поверхні F(x,y,z)=0: ∇F · (r – r₀)=0.
У 3D це основа для поверхонь: нормаль освітлює об’єкти в графіці. Просунуті: у многовидах дотичний простір — лінійний, з метрикою Рімана.
Практичні застосування дотичної
У фізиці миттєва швидкість — дотична до траєкторії. Інженери моделюють аеродинаміку: дотична до крила задає кут атаки. У комп’ютерній графіці нормаль до поверхні рендерить тіні, блиски — без неї ігри плоскі.
У машинному навчанні градієнтний спуск йде по дотичній гіперплощини втрат. Навіть у GPS траєкторії апроксимують дотичними для плавності. Ви не повірите, але ваш смартфон постійно малює дотичні для анімацій.
Цікаві факти про дотичні
- Точка перегину: Крива перетинає горизонтальну дотичну, як у y=x³, але похідні збігаються — парадокс, що ламає старі визначення.
- Стичне коло: Найкраще наближення другого порядку, радіус 1/кривина; еволюта — локація центрів, як “скелет” кривої.
- У мистецтві: Архітектори використовують дотичні для куполів, як у Пантeofна, де вони забезпечують стабільність.
- Сучасний твіст: У AI дотичні моделюють нейронні мережі для генерації реалістичних кривих у графіці (за даними досліджень у комп’ютерній графіці, 2025).
- Рекорд: Замкнуті криві мають ≥4 вершини кривини (теорема чотирьох вершин), пояснюючи форми яєць чи планет.
Дотичні всюди: від крил літаків до кривих на екрані. Вони шепочуть секрети руху, наближення та форми, запрошуючи до нових відкриттів у математиці й житті.