Пряма лінія, що мчить через координатну площину, немов стрімкий потяг по рейках, — це і є графік лінійної функції. У математиці лінійна функція задається простою формулою y = kx + b, де x — незалежна змінна, а y — залежна. Ця модель ідеально описує ситуації, коли зміна однієї величини пропорційна іншій, з фіксованим зсувом. Коефіцієнт k визначає нахил лінії, а b — точку старту на осі y.
Уявіть собі маршрут таксі: відстань зростає рівномірно з часом, але стартова точка — це початковий тариф. Саме так лінійна функція оживає в реальності. Вона універсальна, від шкільних задач до прогнозів у машинному навчанні. Розберемося глибше, чому ця функція — основа багатьох наук.
Область визначення лінійної функції — всі дійсні числа, бо жодних обмежень на x немає. Графік завжди пряма, що робить її легкою для аналізу. Лінійна функція зростає, якщо k > 0, спадає при k < 0 і постійна при k = 0.
Визначення лінійної функції: простота, що ховає силу
Лінійна функція в елементарній математиці — це відношення між змінними, де залежна величина змінюється лінійно від незалежної. Формула y = kx + b фіксує все: пропорційність через k і зсув через b. Якщо b = 0, функція пропорційна, графік через початок координат.
Цікаво, як ця формула еволюціонувала. У вищій математиці лінійна функція переходить у поняття лінійного відображення — оператора, що зберігає додавання та множення на скаляр. Але для школярів і початківців достатньо базового рівня: обчислюйте y для будь-якого x, і отримаєте точку на прямій.
Приклад: для y = 3x – 2, коли x = 1, y = 1; при x = 2, y = 4. Зростання на 3 одиниці за кожну одиницю x — чиста пропорційність з корекцією.
Коефіцієнти лінійної функції: k і b як рушійні сили
K, або кутовий коефіцієнт, показує, на скільки змінюється y при зміні x на 1. Це тангенс кута нахилу до осі x: k = tg α. Велике позитивне k — крутий підйом, як сходи на хмарочос; від’ємне — стрімкий спуск, ніби ковзанка.
B, вільний член, — ордината точки перетину з віссю y, точка (0, b). Вона задає “нульовий” рівень: наприклад, базова зарплата перед преміями. Без b функція проходить через (0,0), ідеальна для пропорцій на кшталт “швидкість × час = шлях”.
- Позитивне k: функція невпинно росте, як акції на буллі.
- Від’ємне k: падає, подібно до витрат на паливо при зростанні цін.
- K=0: горизонтальна лінія, постійна величина, наприклад, фіксована оренда.
Ці коефіцієнти дозволяють прогнозувати: знайшли k і b — і світ у ваших руках. Перевірте на таблиці нижче.
| Тип функції | Приклад | Нахил | Монотонність |
|---|---|---|---|
| y = 2x + 1 | Зростаюча з зсувом | Гострий кут | Зростає |
| y = -0.5x – 3 | Спадна | Тупий кут | Спадна |
| y = 4 | Постійна | Горизонталь | Не змінюється |
Таблиця базується на стандартних властивостях з uk.wikipedia.org. Паралельні лінії мають однакове k, перпендикулярні — добуток k1 × k2 = -1.
Графік лінійної функції: чому завжди пряма лінія
Графік — серце функції. Дві точки визначають пряму, бо функція однозначна. Побудуйте точки (x, y) і з’єднайте — отримайте лінію нескінченною в обидва боки.
Особливості: перетинає вісь y у (0,b), вісь x у точці, де y=0, тобто x = -b/k (якщо k ≠ 0). Це нуль функції, момент, коли все скидається до нуля.
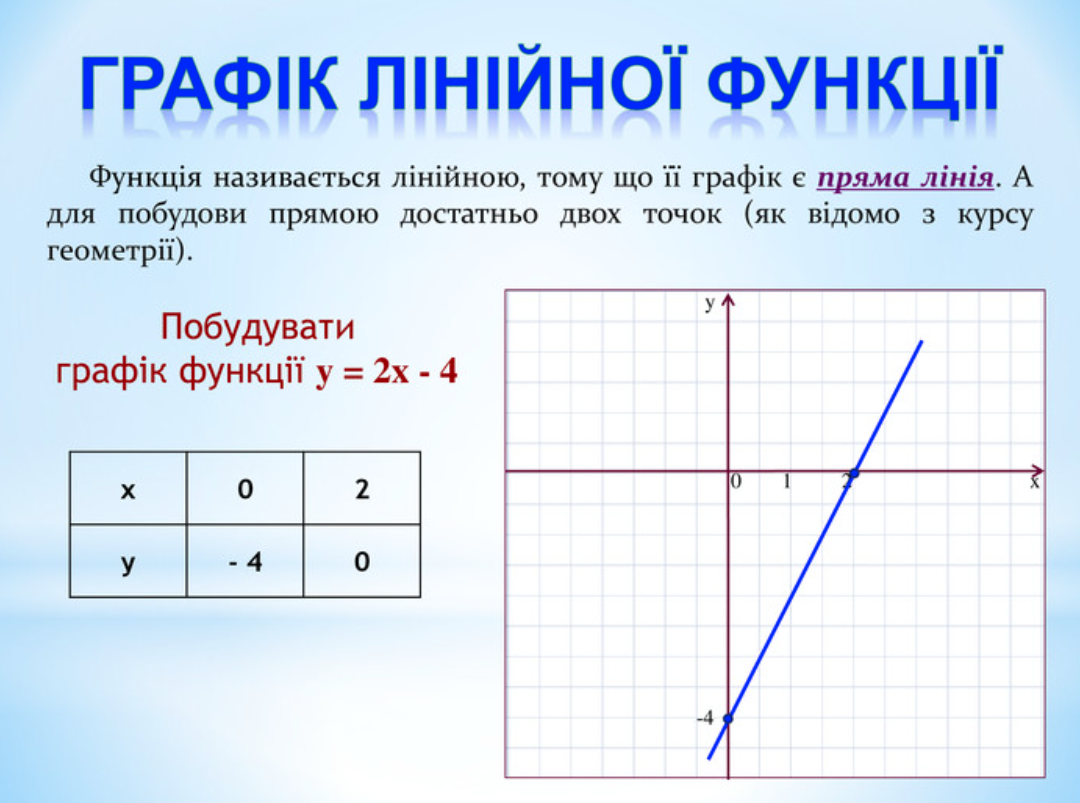
Наприклад, для y = 2x – 4: при x=0, y=-4; при x=2, y=0. Лінія перетинає x у (2,0), спочатку вниз, потім вгору.
Властивості лінійної функції: монотонність і область
Лінійна функція сувора: або завжди росте, або падає, або стоїть на місці. Область значень — всі реальні числа, якщо k ≠ 0; інакше — одне значення b.
- Обчисліть точки: оберіть x=0 і x=1.
- Позначте на площині.
- З’єднайте прямою.
- Проаналізуйте нахил.
Після побудови перевірте: чи проходить через (0,b)? Так — все вірно. Цей ритуал перетворює абстракцію на зорову реальність.
Покрокова побудова графіка лінійної функції
Почніть з таблиці значень. Для y = -x + 3:
| x | y |
|---|---|
| -1 | 4 |
| 0 | 3 |
| 3 | 0 |
Точки (-1,4), (0,3), (3,0) — з’єднайте, і спадаюча лінія готова. Джерело: khanacademy.org. Тепер ви бачите, як графік оживає.
Ви здивуєтеся, наскільки це просто, але потужне знаряддя для візуалізації даних.
Рівняння лінійної функції за двома точками: формула дива
Маєте точки A(x1,y1), B(x2,y2)? Коефіцієнт k = (y2 – y1)/(x2 – x1), потім b = y1 – k x1. Приклад: точки (1,2), (3,6). k = (6-2)/(3-1) = 2, b = 2 – 2*1 = 0. Отже, y=2x.
Ця формула — ключ до регресії: апроксимація даних прямою. У житті точки — спостереження, рівняння — модель.
Історія лінійної функції: від Декарта до алгоритмів
У 1637 році Рене Декарт у “Геометрії” з’єднав алгебру з геометрією, ввівши координатну площину. Раніше лінії малювали без чисел; Декарт зробив їх функціями. Це революція: аналітична геометрія народилася.
Сьогодні лінійні функції — основа GPS, графіки в Excel, прогнози в AI. Без Декарта не було б сучасної інформатики.
Практичні кейси: лінійна функція в дії
У фізиці: шлях s = v t, де v — швидкість (k), початковий шлях=0. Автомобіль на 60 км/год: s=60t. За годину — 60 км.
Економіка: витрати C = 100 + 5n, де 100 — фікс, 5 грн за одиницю товару n. Виробили 20 — 200 грн витрат.
Програмування: у Python def linear(x): return 2*x + 1. Моделі в TensorFlow починаються з лінійної регресії для прогнозів продажів 2026 року.
Температура: перетворення Цельсій-Фаренгейт F=1.8C + 32. k=1.8 — коеф. розширення.
Ці приклади показують: лінійна функція — місток від теорії до практики. Спробуйте самі змоделювати свій день!
Лінійна функція в машинному навчанні та сучасних трендах
У 2026 році лінійна регресія — стартова точка ML. Прогнозуйте ціни житла: y = k1*площа + k2*район + b. Алгоритми мінімізують помилки, знаходячи ідеальні k і b.
У бізнесі: оптимізація логістики, де витрати пропорційні відстані. Навіть у екології моделі забруднення повітря лінійні на коротких інтервалах.
Ви не повірите, але проста шкільна функція лежить в основі ChatGPT — у базових шарах нейромереж.
Розв’язання типових задач на лінійні функції
Задача: знайдіть k і b для лінії через (0,5) і (2,9). k=(9-5)/(2-0)=2, b=5. y=2x+5.
- Графік перетинає осі? x=-b/k, y=b.
- Паралельна до y=3x+1? Така ж k=3.
- Перпендикулярна? k2=-1/3.
Ці інструменти роблять вас майстром. Експериментуйте з Desmos чи GeoGebra — і математика заграє новими фарбами.
Лінійна функція кличе до відкриттів: від графіка до глобальних прогнозів. Де ще ховається її магія в вашому житті?






