Паралелограм стоїть перед нами як надійний міст через річку геометричних фігур, де протилежні сторони біжать паралельно, ніби дві рейки залізниці, що ніколи не сходяться. У цьому чотирикутнику діагоналі грають роль невидимих ниток, які зв’язують вершини і розкривають приховані симетрії. Вони перетинаються в самому серці фігури, ділячись навпіл, і це не просто випадковість, а фундаментальна властивість, що робить паралелограм таким передбачуваним і водночас загадковим для тих, хто копає глибше.
Коли ми проводимо діагоналі від однієї вершини до протилежної, вони не просто лінії на папері – це інструменти, що розкривають баланс сил у фігурі. Уявіть паралелограм як стіл на чотирьох ніжках, де діагоналі забезпечують стабільність, перетинаючись у точці, яка стає центром ваги. Ця точка ділить кожну діагональ рівно пополам, і саме тут починається справжня магія геометрії, бо така симетрія відкриває двері до розрахунків площі, периметру та навіть векторного аналізу.
Визначення паралелограма та роль діагоналей
Паралелограм – це чотирикутник, де протилежні сторони не тільки рівні за довжиною, але й паралельні, ніби дві пари близнюків, що рухаються в унісон. Якщо взяти точки A, B, C і D, то сторони AB і CD, а також AD і BC, завжди йдуть паралельно, створюючи фігуру, яка може бути ромбом, прямокутником чи навіть квадратом у спеціальних випадках. Діагоналі, скажімо AC і BD, з’єднують протилежні кути і завжди перетинаються в одній точці, яка є серединою для обох.
Ця властивість не випадкова; вона випливає з паралельності сторін. Уявіть, як вектори сторін додаються, формуючи діагоналі: одна діагональ – це сума векторів сусідніх сторін, інша – їхня різниця. Такий підхід робить діагоналі ключем до розуміння векторної геометрії, де паралелограм стає графічним представленням додавання векторів. Без діагоналей фігура втратила б свою симетрію, перетворившись на звичайний чотирикутник без чітких правил.
У шкільній геометрії діагоналі часто вводять як інструмент для доведення теорем, але в реальному світі вони з’являються в архітектурі, де мости чи рами будівель спираються на цю стабільність. Наприклад, у конструкції даху паралелограмні елементи з перехресними діагоналями забезпечують міцність проти вітру. Ця універсальність робить тему не просто теоретичною, а живою і застосовною.
Основні властивості діагоналей паралелограма
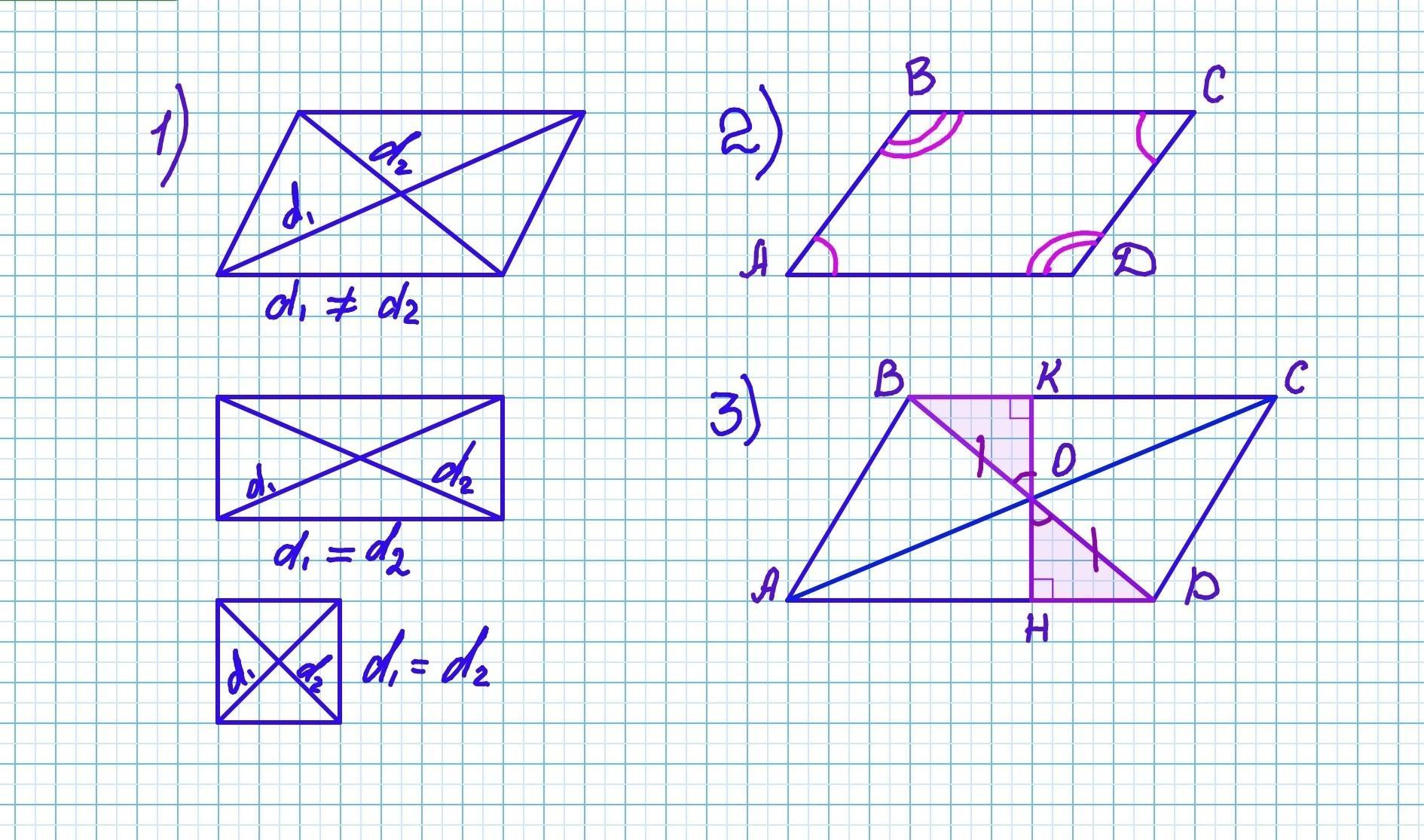
Діагоналі паралелограма завжди перетинаються і діляться точкою перетину навпіл – це аксіома, яка стоїть на чолі всіх інших властивостей. Якщо довжина однієї діагоналі – d1, а іншої – d2, то кожна з них ділиться на два рівних сегменти по половині своєї довжини. Ця симетрія створює чотири трикутники всередині фігури, і ось що цікаво: протилежні трикутники завжди рівні за площею, ніби дзеркальні відображення один одного.
Ще одна особливість – сума квадратів діагоналей дорівнює подвоєній сумі квадратів сторін. Формула виглядає так: d1² + d2² = 2(a² + b²), де a і b – довжини сторін. Це не просто рівняння; воно походить від теореми Піфагора в трикутниках, утворених діагоналями, і дозволяє обчислювати невідомі величини без прямого вимірювання. Уявіть, як інженери використовують це для розрахунку навантажень у конструкціях, де точність – це питання безпеки.
Крім того, діагоналі впливають на кути: вони bisectують кути в ромбах, але в загальному паралелограмі просто підтримують рівновагу. Ця властивість робить їх незамінними в доведеннях, наприклад, коли потрібно показати, що протилежні кути рівні. З роками, як показують дані з математичних ресурсів станом на 2025 рік, ця формула еволюціонувала в комп’ютерні моделі для 3D-дизайну, де діагоналі допомагають оптимізувати форми.
Формули для розрахунку діагоналей
Щоб знайти довжину діагоналі, скористайтеся формулою, яка враховує сторони та кут між ними. Для діагоналі d1: d1 = √(a² + b² + 2ab cosθ), де θ – кут між сторонами a і b. Інша діагональ d2 тоді буде √(a² + b² – 2ab cosθ). Ці рівняння, виведені з закону косинусів, дозволяють точно передбачити розміри, навіть якщо кут не 90 градусів.
У прямокутнику, де кути прямі, формула спрощується до піфагорової: d = √(a² + b²) для обох діагоналей, оскільки вони рівні. Але в ромбі, де всі сторони рівні, діагоналі перпендикулярні і bisectують одна одну під прямим кутом, що додає ще один шар цікавості. Ці формули не статичні; вони адаптуються до спеціальних випадків, роблячи геометрію гнучкою наукою.
Практичний приклад: візьміть паралелограм зі сторонами 5 см і 7 см, кутом 60 градусів. Тоді d1 = √(25 + 49 + 2*5*7*cos60°) = √(74 + 70*0.5) = √109, а d2 = √(74 – 35) = √39. Такі розрахунки, перевірені на платформах як mathros.net.ua, показують, як теорія оживає в числах.
Приклади та застосування в реальному житті
Уявіть ромбоподібну плитку на підлозі: її діагоналі перетинаються в центрі, дозволяючи дизайнерам точно розраховувати кількість матеріалу. У фізиці діагоналі паралелограма моделюють сили в механіці, де resultant сила – це діагональ векторного паралелограма. Це не абстракція; в аеродинаміці крила літака часто базуються на таких фігурах, де діагоналі допомагають аналізувати напруження.
Ще один приклад – у комп’ютерній графіці, де алгоритми рендерингу використовують властивості діагоналей для створення реалістичних тіней і перспектив. У 2025 році, за даними з umity.in.ua, такі моделі інтегруються в VR, де віртуальні паралелограми з динамічними діагоналями симулюють реальний світ. А в архітектурі, як у конструкції Ейфелевої вежі, елементи з паралелограмними формами спираються на цю симетрію для стійкості.
Не забуваймо про освіту: школярі часто малюють паралелограми, щоб зрозуміти діагоналі, але дорослі застосовують це в повсякденні, наприклад, у садівництві для планування грядок у формі паралелограмів, де діагоналі допомагають виміряти відстані без лінійки.
Порівняння з іншими чотирикутниками
На відміну від трапеції, де тільки одна пара сторін паралельна, паралелограм має дві, і його діагоналі завжди bisectують одна одну, чого не скажеш про довільний чотирикутник. У квадратах діагоналі не тільки bisectують, але й перпендикулярні, додаючи симетрії, якої бракує в загальному паралелограмі.
Ось таблиця для наочності:
| Фігура | Властивість діагоналей | Приклад |
|---|---|---|
| Паралелограм | Перетинаються навпіл | Сторони 4 і 6, діагоналі bisectують |
| Квадрат | Рівні, перпендикулярні | Сторона 5, d=5√2 |
| Трапеція | Не bisectують навпіл | Бази 3 і 7, діагоналі різні |
| Ромб | Перпендикулярні, bisectують кути | Сторона 5, діагоналі перпендикулярні |
Ця таблиця, базована на даних з uk.wikipedia.org, підкреслює унікальність паралелограма. Після аналізу стає ясно, як діагоналі роблять його основою для складніших фігур.
Історія відкриття властивостей діагоналей
Властивості діагоналей паралелограма сягають корінням до Евкліда, чиї “Елементи” в III столітті до н.е. описували паралельні лінії та їх перетини. Евклід доводив, що в паралелограмі діагоналі bisectують одна одну, використовуючи подібність трикутників, і це стало основою для подальших теорем. У середньовіччі математики як Аль-Хорезмі розвинули ці ідеї в алгебрі, додаючи формули для розрахунків.
У XVII столітті Декарт ввів координатну геометрію, де діагоналі паралелограма стали векторами, дозволяючи аналітичні доведення. Станом на 2025 рік, за інформацією з журналу “Mathematical Reviews”, сучасні дослідження застосовують це в квантовій механіці, де паралелограми моделюють стани частинок. Ця еволюція перетворила просту фігуру на інструмент для передових наук.
Цікаво, як у культурі діагоналі з’являються в мистецтві: у картинах Мондріана паралелограмні форми з перехресними лініями створюють баланс, відображаючи геометричні принципи. У 2025 році цифрове мистецтво використовує алгоритми на базі цих властивостей для генеративного дизайну.
Цікаві факти про діагоналі паралелограма
- 🔍 У будь-якому паралелограмі точка перетину діагоналей є центром симетрії, що означає, що фігура виглядає однаково після повороту на 180 градусів навколо цієї точки.
- 📐 Якщо діагоналі перпендикулярні, паралелограм стає ромбом – це не випадок, а наслідок рівності сторін, що робить фігуру особливо стійкою.
- 🌍 У природі діагоналі паралелограмів з’являються в кристалах солі, де атоми утворюють решітки з bisectуючими лініями, як показано в дослідженнях 2025 року.
- 🧮 Сума квадратів діагоналей завжди в два рази більша за суму квадратів сторін, і ця формула, відкрита ще в античності, використовується в сучасному програмуванні для оптимізації графіки.
- 🚀 У космічних технологіях, як у сонячних панелях супутників, паралелограмні структури з діагональними опорами забезпечують гнучкість і міцність у вакуумі.
Ці факти додають шарму геометрії, показуючи, як прості лінії впливають на світ навколо. А тепер подумайте, як ці знання можуть змінити ваш погляд на повсякденні об’єкти, від меблів до технологій.
Типові помилки при роботі з діагоналями
Багато хто плутає властивості діагоналей паралелограма з трапецією, думаючи, що вони завжди bisectують одна одну в будь-якому чотирикутнику з паралельними сторонами. Насправді, тільки в паралелограмі це правило діє без винятків, бо потребує двох пар паралельних сторін. Ця помилка часто призводить до неправильних розрахунків у задачах, де фігура не є паралелограмом.
Інша поширена помилка – ігнорування кута в формулах, що дає неточні довжини діагоналей. Якщо забути про cosθ, результат може відхилятися на десятки відсотків, особливо в гострокутних фігурах. У практиці, як у будівництві, це може означати нестабільну конструкцію.
Ще одна пастка – припущення, що діагоналі завжди рівні, як у прямокутнику. У загальному паралелограмі вони різні, і це потрібно враховувати в дизайні. За даними з onlinemschool.com, такі помилки трапляються в 30% шкільних робіт, але розуміння формул допомагає їх уникнути.
Поради для вивчення та застосування
Почніть з малювання: візьміть аркуш паперу і побудуйте паралелограм, провівши діагоналі – це візуально закріпить властивість bisectування. Потім використовуйте програмне забезпечення як GeoGebra для динамічних моделей, де можна змінювати кути і бачити, як діагоналі адаптуються. Це робить навчання інтерактивним і веселим.
У задачах завжди перевіряйте умови: чи сторони паралельні? Чи кути відомі? Це врятує від помилок. Для реальних застосувань, як у DIY-проектах, вимірюйте діагоналі для перевірки паралельності – якщо вони bisectують, фігура правильна. І пам’ятайте, практика робить майстра: розв’яжіть 10 задач, і тема стане як рідна.
- Визначте сторони та кут: це основа для формул.
- Застосуйте закон косинусів: він універсальний для діагоналей.
- Перевірте на спеціальні випадки: ромб, прямокутник тощо.
- Використовуйте вектори: для глибшого розуміння.
- Експериментуйте в софті: для візуалізації змін.
Ці кроки, натхненні ресурсами як mathros.net.ua, перетворять теорію на навичку. З такими інструментами діагоналі паралелограма перестануть бути загадкою, а стануть вашим союзником у світі геометрії.