Великий квадрат мінус менший квадрат перетворюється на простий добуток двох виразів — ось у чому чарівність формули a² – b² = (a – b)(a + b). Ця тотожність, ніби гострий ніж, ріже складні вирази на частини, роблячи математику легшою та елегантнішою. Вона з’являється скрізь: від шкільних задач до криптографічних алгоритмів, де секунди вирішують безпеку даних.
Уявіть площу квадрата зі стороною a, з якої віднімаємо площу квадрата b. Результат не просто число — це прямокутник, розбитий на дві частини, які легко перемножити. Така геометрична інтуїція робить формулу не сухою аксіомою, а живим інструментом.
Корені формули: подорож від Вавилону до Евкліда
Ще за 1800 років до нашої ери вавилоняни розв’язували квадратичні рівняння, стикаючись з різницею квадратів у геометричних задачах на поля. Вони не записували формулу символічно, але використовували її для обчислень площ і об’ємів. Евклід у “Початках” (Книга II, пропозиції 5-6) довів її геометрично, перетворюючи абстрактну алгебру на малюнки з квадратами та прямокутниками.
У Середньовіччі арабські математики, як аль-Хорезмі, систематизували ці ідеї в алгебрі, де формула стала основою для факторізації. Сьогодні, за даними mathshistory.st-andrews.ac.uk, вона лишається фундаментом, еволюціонуючи в комп’ютерні алгоритми. Ця давня знахідка досі рятує програмістів від нескінченних обчислень.
Доведення, що переконує: алгебра проти геометрії
Розкрийте дужки в (a – b)(a + b): a·a + a·b – b·a – b·b. ab і ba скасовуються за комутативністю, лишаючи a² – b². Просто, елегантно, бездоганно — ось алгебраїчне доведення, яке працює в будь-якому комутативному кільці, як зазначає uk.wikipedia.org.
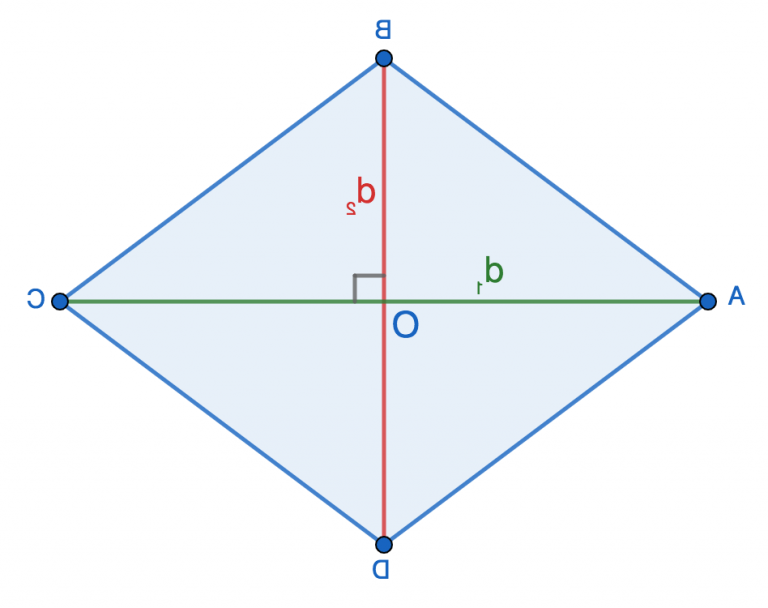
Геометрія додає візуальний шарм. Великий квадрат a×a мінус b×b — це L-подібна фігура. Розріжте її на два прямокутники: один a×(a-b), другий b×(a-b). Винесіть спільний множник (a-b), отримайте (a + b)(a – b). Евклід малював це на піску, а ми — у уяві.
Обидва підходи доповнюють один одного: алгебра для швидкості, геометрія для інтуїції. Спробуйте самі — малюнок переверне ваше сприйняття.
Перші кроки: базові приклади, що запам’ятовуються
Почніть з класики: 9² – 4² = 81 – 16 = 65. За формулою: (9-4)(9+4) = 5·13 = 65. Швидко й без калькулятора.
Змінні додають гостроти. x² – 25 = (x – 5)(x + 5). Тут 25 = 5², ідеальний квадрат. Або 16x² – y² = (4x – y)(4x + y). Перед списком прикладів згадайте: завжди шукайте квадрати під знаком мінус.
- Обчислення: (3x + 2)² – (3x – 2)². Ні, це не пряма різниця, але розкрийте: 4·3x·2 = 24x.
- Факторизація: 49 – 36z² = (7 – 6z)(7 + 6z). Перевірте множенням.
- З константами: 100 – 4a⁴ = (10 – 2a²)(10 + 2a²), спрощуйте далі.
Ці приклади, натхненні уроками khanacademy.org, показують, як формула економить час. Тепер переходьте до складнішого.
Поліноми вищих степенів: розкладання як гра в кубики
Коли вираз — x⁴ – 16, бачите (x²)² – 4² = (x² – 4)(x² + 4). Далі x² – 4 = (x – 2)(x + 2). Результат: (x – 2)(x + 2)(x² + 4). Ланцюгова реакція множників!
Таблиця нижче порівнює формули скороченого множення для наочності. Вона допомагає обрати інструмент швидко.
| Формула | Вираз | Приклад |
|---|---|---|
| Різниця квадратів | a² – b² = (a – b)(a + b) | x² – 9 = (x – 3)(x + 3) |
| Квадрат суми | (a + b)² = a² + 2ab + b² | (x + 2)² = x² + 4x + 4 |
| Квадрат різниці | (a – b)² = a² – 2ab + b² | (x – 1)² = x² – 2x + 1 |
| Різниця кубів | a³ – b³ = (a – b)(a² + ab + b²) | 8 – y³ = (2 – y)(4 + 2y + y²) |
Джерела даних: uk.wikipedia.org та khanacademy.org. Таблиця ілюструє, як різниця квадратів — найпростіша, але потужна. Використовуйте її для многочленів 4-го степеня, як x⁴ – 81 = (x² – 9)(x² + 9) = (x – 3)(x + 3)(x² + 9).
Розв’язок рівнянь: де формула сяє яскраво
Рівняння x² – 25 = 0 стає (x – 5)(x + 5) = 0, корені x=5, x=-5. Миттєво! Складніше: 4x⁴ – 36x² + 81 = 0. Підстановка y = x², отримуємо 4y² – 36y + 81. Дискримінант негативний? Ні, факторизуйте як різницю.
У задачах на площі чи швидкості формула спрощує: наприклад, у фізиці різниця швидкостей v₁² – v₂² = (v₁ – v₂)(v₁ + v₂) для роботи двигунів. Практично й точно.
Комплексний світ та раціоналізація: розширюємо горизонти
Сума квадратів? Додайте i: x² + 4 = x² – (2i)² = (x – 2i)(x + 2i). Ідеально для коренів поліномів. Раціоналізація знаменника 1/√a – √b множиться на кон’югат, даючи різницю квадратів у чисельнику.
У криптографії Fermatів метод факторизації RSA використовує n = x² – y² для великих чисел, як описано в математичних текстах. Формула перетворює “неможливе” на реальність.
🚫 Типові помилки початківців
- 😵💫 Плутанина з сумою квадратів: a² + b² не факторизується просто — це пастка. Перевіряйте знак мінус!
- ❌ Забули витягти коефіцієнти: У 9x² – 4 = (3x)² – 2², а не (9x – 2)(9x + 2). Завжди шукайте досконалі квадрати.
- 🔄 Порядок множників: (a + b)(a – b), не навпаки — інакше знак зміниться.
- 📉 Ігнор вищих степенів: x⁴ + 4 не різниця, але x⁴ – 16 — так. Групуйте правильно.
- ⚠️ Не перевіряєте: Завжди множте назад, щоб уникнути помилок.
Цей блок врятує години на контрольних. Уникайте цих ям — і алгебра стане другом.
Поради від практика: як опанувати формулу назавжди
Тренуйтеся на щоденних задачах: генеруйте випадкові a та b, факторизуйте. Використовуйте в рівняннях 2-го та 4-го степенів — 80% шкільних задач піддаються. У програмуванні імплементуйте для символьних обчислень у Python чи Mathematica.
Комбінуйте з іншими формулами: після різниці — куби чи триноми. Реальні задачі, як оптимізація в економіці (різниця прибутків), оживають з нею. Ви не повірите, наскільки це addictive!
Формула різниці квадратів — не просто правило, а місток між давниною й майбутнім математики. Експериментуйте, і вона розкриє нові грані.