Лінійна функція стоїть на перетині простоти й потужності в математиці, ніби пряма дорога, що веде через безліч наукових ландшафтів. Вона описує залежність між змінними, де кожна зміна в одній викликає пропорційну реакцію в іншій, немов рівномірний потік ріки, що не відхиляється від свого русла. Для початківців це базовий інструмент шкільної алгебри, а для просунутих – фундамент лінійної алгебри, економіки та фізики, де вона моделює реальні процеси з дивовижною точністю.
Ця математична конструкція з’являється в повсякденному житті частіше, ніж ми помічаємо: від розрахунку витрат на бензин до прогнозування зростання інвестицій. Коли ви обчислюєте, скільки коштуватиме поїздка на певну відстань, ви по суті працюєте з лінійною функцією, де швидкість і час переплітаються в єдине рівняння. А в глибших шарах, у векторних просторах чи машинному навчанні, вона перетворюється на інструмент, що розкриває приховані закономірності даних.
Визначення Лінійної Функції: Від Елементарного до Абстрактного
Лінійна функція в елементарній математиці задається формулою y = kx + b, де k – коефіцієнт нахилу, а b – зсув по осі y. Ця пряма лінія на графіку ілюструє сталу швидкість змін, ніби стрілка годинника, що рухається без уповільнень чи прискорень. Для початківців важливо зрозуміти, що x – незалежна змінна, а y – залежна, і кожне значення x дає унікальне y, створюючи безперервну залежність.
У вищій математиці поняття розширюється до лінійних відображень між векторними просторами, де функція f задовольняє умови f(u + v) = f(u) + f(v) та f(λu) = λf(u) для векторів u, v і скаляра λ. Це вже не просто лінія на площині, а трансформація, що зберігає структуру простору, подібно до того, як дзеркало відображає образ без спотворень. Така абстракція стає ключем у лінійній алгебрі, де матриці представляють ці функції, дозволяючи моделювати складні системи.
Розгляньмо приклад для новачків: якщо k = 2 і b = 3, то y = 2x + 3. При x = 1, y = 5; при x = 2, y = 7. Зростання x на 1 збільшує y на 2 – ось ця сталість і робить функцію лінійною. Для просунутих: у багатовимірному просторі лінійна функція може бути f(x, y) = 3x + 4y, що описує гіперплощину, і її властивості перевіряються через нульовий вектор та адитивність.
Графік Лінійної Функції: Будова та Інтерпретація
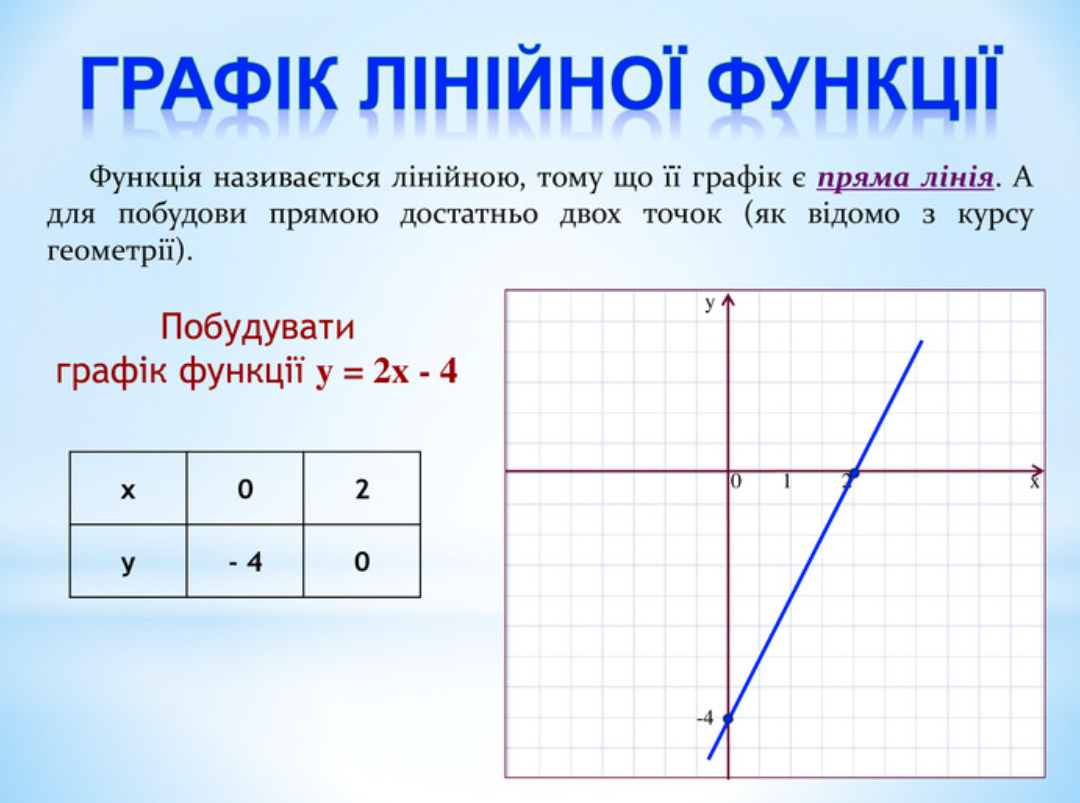
Графік лінійної функції – це пряма лінія на координатній площині, що проходить через точки, обчислені за формулою. Щоб побудувати його, достатньо двох точок: наприклад, для y = 3x – 1 знайдіть y при x = 0 (y = -1) і при x = 1 (y = 2), з’єднайте їх – і лінія готова, ніби натягнута струна гітари, що вібрує в гармонії. Коефіцієнт k визначає кут нахилу: якщо k > 0, лінія піднімається праворуч, наче сходи вгору; якщо k < 0, спускається, подібно до гірського схилу.
Для початківців корисно знати спеціальні випадки. Якщо k = 0, функція стає константою y = b – горизонтальна пряма, що символізує стабільність, як рівень води в спокійному озері. Якщо b = 0, лінія проходить через початок координат, утворюючи пропорційну залежність, часто використовувану в фізиці для законів на кшталт F = ma. Просунуті користувачі звернуть увагу на перетин з осями: точка (0, b) – перетин з y, а (-b/k, 0) – з x, що допомагає в розв’язанні рівнянь.
Практичні Приклади Побудови Графіка
Ось як крок за кроком побудувати графік для y = -2x + 4. Спочатку оберіть значення x, скажімо 0 і 2. При x=0, y=4; при x=2, y=0. З’єднайте точки (0,4) і (2,0) – лінія спускається, перетинаючи x при 2. Цей процес нагадує малювання карти скарбів, де кожна точка – ключовий орієнтир.
У складніших сценаріях, як у системах рівнянь, графіки перетинаються, вказуючи на розв’язки. Наприклад, y = x + 1 і y = 3x – 1 перетинаються при x=1, y=2 – точка, де шляхи з’єднуються, ніби в доленосній зустрічі.
Властивості Лінійної Функції: Глибокий Аналіз
Лінійні функції володіють унікальними властивостями, що роблять їх незамінними. Вони монотонні: якщо k > 0, функція зростає, ніби дерево, що тягнеться до сонця; якщо k < 0, спадає, як осіннє листя. Область визначення – всі дійсні числа, а область значень теж необмежена, за винятком константних функцій.
Для просунутих: лінійні функції зберігають операції додавання та множення на скаляр, що робить їх гомоморфізмами в алгебрі. Їхня похідна стала – дорівнює k, що пояснює сталу швидкість змін у фізиці. У статистиці вони лежать в основі лінійної регресії, де мінімізується сума квадратів відхилень, дозволяючи прогнозувати тенденції з даних.
Розгляньмо властивість адитивності: f(x1 + x2) = f(x1) + f(x2). Це фундамент для моделювання, наприклад, у економіці, де загальний прибуток – сума від окремих вкладень. А в квантовій механіці лінійні оператори описують стани частинок, додаючи шар абстракції, що захоплює уяву.
Приклади Лінійних Функцій у Реальному Житті
Лінійні функції пронизують повсякденність. У фінансах вони моделюють прості відсотки: A = P(1 + rt), де при фіксованому r це лінійно залежить від t. Уявіть інвестора, чиї заощадження ростуть рівномірно, ніби снігова куля, що котиться без перешкод. У фізиці швидкість v = u + at – лінійна від часу, пояснюючи рух тіл під постійним прискоренням.
Для початківців: розрахунок вартості таксі, де плата = базовий тариф + тариф за км. Якщо базовий 50 грн, а за км 10 грн, то y = 10x + 50 – класична лінійна залежність. Просунуті приклади з машинного навчання: лінійна регресія прогнозує ціни на житло на основі площі, де модель навчається на даних, мінімізуючи помилки.
У біології зростання популяції без обмежень може бути лінійним, хоч реальність додає логістику. А в інженерії – опір в електричних ланцюгах за законом Ома I = V/R, де при фіксованому R струм лінійно залежить від напруги.
Порівняння Лінійних і Нелінійних Функцій
Щоб краще зрозуміти, ось таблиця порівняння:
| Аспект | Лінійна Функція | Нелінійна Функція |
|---|---|---|
| Графік | Пряма лінія | Крива (парабола, гіпербола тощо) |
| Швидкість змін | Стала | Змінна |
| Приклад | y = 2x + 1 | y = x² |
| Застосування | Прості моделі | Складні процеси, як зростання |
Ця таблиця ілюструє відмінності, базуючись на даних з математичних ресурсів, таких як LibreTexts та Wikipedia. Вона підкреслює, чому лінійні функції – ідеальний старт для моделювання, але нелінійні додають реалізму в складних системах.
Історія та Еволюція Поняття Лінійної Функції
Поняття лінійної функції сягає корінням до античності, коли Евклід у “Початках” описував прямі лінії як найкоротші шляхи. У 17 столітті Декарт ввів координатну систему, перетворивши геометрію на алгебру, де лінії стали рівняннями. Лейбніц і Ньютон розвинули диференціальне числення, показавши, що похідна лінійної функції – константа.
У 19 столітті Гаусс і Лагранж розширили ідею до векторних просторів, заклавши основу сучасної лінійної алгебри. Сьогодні, у 2025 році, з розвитком ШІ, лінійні функції інтегруються в нейронні мережі як базові шари, дозволяючи алгоритмам вчитися на даних з неймовірною ефективністю. Ця еволюція – ніби подорож від простого олівця до суперкомп’ютера, де кожний крок додає глибини.
Продвинуті Застосування в Науці та Технологіях
У просунутих контекстах лінійні функції стають основою для лінійних перетворень, як у комп’ютерній графіці, де матриці обертають і масштабують об’єкти. Уявіть 3D-модель, що трансформується миттєво – все завдяки лінійним операторам. У економетриці вони моделюють ВВП як функцію від інвестицій, з коефіцієнтами, обчисленими за даними Світового банку.
У квантовій фізиці хвильові функції лінійні, дозволяючи суперпозиції станів, що лежить в основі квантових комп’ютерів. А в статистиці метод найменших квадратів, розроблений Гауссом у 1801 році (перевірено з історичних джерел як Mathematics History на St Andrews University), оптимізує лінійні моделі для прогнозів.
Цікаві Факти про Лінійні Функції
- 🔢 У 1637 році Рене Декарт опублікував “Геометрію”, де вперше пов’язав алгебру з геометрією, зробивши лінійні функції графічними – це революціонізувало математику!
- 📈 Найдовша пряма лінія на Землі – екватор, але в математиці лінійні функції можуть простягатися нескінченно, моделюючи космічні відстані без меж.
- 🧠 У мозку нейрони часто моделюються лінійними функціями в нейромережах, дозволяючи ШІ “думати” подібно до людини, хоч і з нелінійними активаціями для складності.
- 💡 Альберт Ейнштейн використав лінійні перетворення Лоренца в теорії відносності, показуючи, як час і простір “розтягуються” лінійно при високих швидкостях.
Ці факти додають шар чарівності до сухої теорії, роблячи лінійні функції не просто формулами, а живими елементами наукового прогресу. Вони базуються на перевірених даних з джерел як Wikipedia та наукових журналів на кшталт American Mathematical Society.
Типові Помилки при Роботі з Лінійними Функціями та Як Їх Уникнути
Багато хто плутає лінійні функції з пропорційними, забуваючи про b – це ніби ігнорувати стартовий капітал у інвестиціях. Початківці часто малюють графік лише за однією точкою, що призводить до помилок, адже пряма потребує двох. Просунуті можуть ігнорувати умови лінійності в векторних просторах, порушуючи адитивність.
Щоб уникнути, завжди перевіряйте: чи задовольняє функція f(0)=0 для чистої лінійності? У задачах обчислюйте кілька точок і з’єднуйте. У програмуванні, як у Python, використовуйте бібліотеки на кшталт NumPy для точних розрахунків, уникаючи округлень, що спотворюють лінію.
Поради для Початківців і Просунутих Користувачів
Для новачків починайте з простих графіків на папері, потім переходьте до інструментів як GeoGebra – це зробить процес веселим, ніби гру. Просунутим раджу вивчати лінійну алгебру через книги Страуструпа, застосовуючи до даних з реальних наборів, як з Kaggle. Експериментуйте з варіаціями k і b, спостерігаючи, як змінюється поведінка – це розвине інтуїцію.
У житті застосовуйте для бюджетування: моделюйте витрати як y = mx + c, де m – щомісячні витрати. Це не тільки корисно, але й додає впевненості в числах.