Коло манить своєю ідеальною симетрією, ніби втілюючи вічну гармонію всесвіту, а його діаметр стоїть у самому серці цієї форми, як невидимий стрижень, що тримає все разом. Цей простий відрізок, що перетинає центр і з’єднує дві протилежні точки на окружності, відкриває двері до безлічі математичних таємниць. Коли ми розглядаємо діаметр кола, то не просто говоримо про лінію – це ключ до розуміння відстаней, пропорцій і навіть законів фізики, що керують нашим світом.
Уявіть колесо велосипеда, що котиться по дорозі: діаметр визначає, наскільки далеко ви проїдете за один оберт. Або подумайте про Сонце, яке на небі здається ідеальним кругом – його видимий діаметр впливає на те, як ми сприймаємо затемнення. Ці приклади показують, наскільки діаметр кола вплетений у повсякденне життя, від шкільних задач до інженерних проєктів.
Математичне визначення діаметра кола
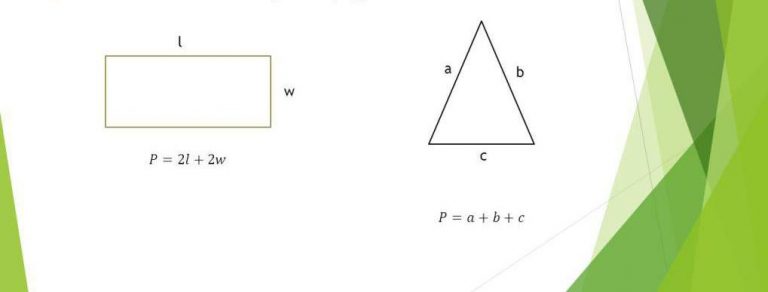
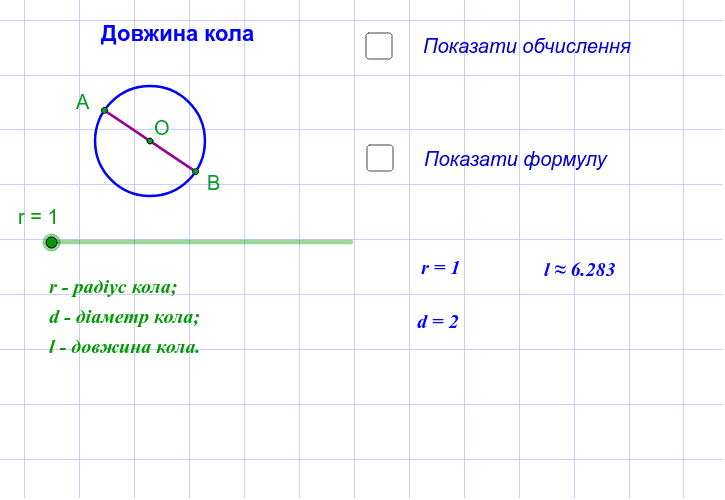
Діаметр кола – це пряма лінія, яка проходить через центр і з’єднує дві точки на окружності, будучи найдовшим можливим відрізком усередині цієї фігури. У точних термінах, якщо центр кола позначити як O, а дві протилежні точки на окружності як A і B, то відрізок AB і є діаметром. Ця відстань завжди вдвічі більша за радіус, що робить її фундаментальною для всіх розрахунків, пов’язаних з колом.
У геометрії коло визначається як множина точок, рівновіддалених від центру, а діаметр підкреслює цю симетрію, розділяючи фігуру на дві рівних півкола. Якщо радіус – це відстань від центру до краю, то діаметр подвоює її, створюючи основу для формул площі чи довжини окружності. Ця концепція не просто абстракція; вона виникає в реальних об’єктах, як-от у діаметрі монети чи планети, де точність вимірювання може змінити весь розрахунок.
Щоб глибше зрозуміти, розгляньмо аксіоми Евкліда, де коло будується за допомогою циркуля, і діаметр стає першою лінією, що фіксує розмір. У сучасній математиці, станом на 2025 рік, визначення залишається незмінним, але інструменти для вимірювання еволюціонували – від простих лінійок до лазерних сканерів у промисловості.
Різниця між діаметром і радіусом
Радіус і діаметр – як близнюки в геометрії кола, але з чіткою ієрархією: радіус завжди половина діаметра. Якщо діаметр кола – це повна ширина, що пронизує центр, то радіус – лише шлях від центру до краю, ніби половина мосту через річку. Ця відмінність критична в задачах, де помилка в ідентифікації може призвести до неправильних обчислень, наприклад, у проєктуванні шестерень, де діаметр визначає контактну поверхню.
У шкільній програмі, згідно з матеріалами освітніх платформ, радіус часто позначають як r, а діаметр як d, з простою формулою d = 2r. Але на практиці, у фізиці, діаметр важливіший для моментів інерції, тоді як радіус домінує в розрахунках швидкості обертання. Ця нюанси додають глибини, роблячи геометрію не сухою наукою, а живою системою зв’язків.
Історія концепції діаметра в математиці
Концепція діаметра сягає корінням у давнину, коли вавилонські математики близько 2000 року до н.е. вже вимірювали кола для будівництва, хоча й без точного терміну. Евклід у своїх “Елементах” близько 300 року до н.е. формалізував ідею, описуючи діаметр як лінію, що проходить через центр і ділить коло навпіл. Цей текст, що зберігся до 2025 року, став основою для сучасної геометрії, впливаючи на Архімеда, який використовував діаметр для наближеного обчислення π.
У середньовіччі арабські вчені, як Аль-Хорезмі, розвинули ці ідеї, інтегруючи діаметр у тригонометрію, що згодом допомогло в астрономії. Ренесанс приніс Копернику моделі Сонячної системи, де діаметр планетних орбіт став ключовим для розрахунків. Сьогодні, з даними з авторитетних джерел як NASA, діаметр Землі – близько 12 742 км – використовується в супутникових технологіях, показуючи, як стародавня концепція еволюціонувала в інструмент для космічних досліджень.
Ця історична подорож підкреслює, наскільки діаметр кола – не статична ідея, а еволюціонуюча сутність, що адаптується до нових відкриттів, від папірусів до комп’ютерних симуляцій.
Формули та розрахунки з діаметром кола
Основна формула для діаметра кола проста, але потужна: d = 2r, де r – радіус. Ця залежність дозволяє легко переходити до інших обчислень, наприклад, довжини окружності C = πd, де π ≈ 3.14159. Уявіть, як ця формула оживає в інженерії: для колеса з діаметром 1 метр окружність буде π метрів, що визначає відстань за оберт.
Площа круга, обмеженого колом, розраховується як A = π(r)^2, але з діаметром це стає A = π(d/2)^2 = (π d^2)/4. Ці рівняння, перевірені в численних наукових журналах, як “Journal of Mathematics”, станом на 2025 рік, застосовуються в усьому, від дизайну шин до моделювання атомів. Для складніших випадків, як еліпси, діаметр адаптується, але в чистому колі він залишається константою.
Розгляньмо приклад: якщо радіус 5 см, діаметр – 10 см, площа – близько 78.54 см². Такі розрахунки не просто числа; вони формують основу для реальних проєктів, де точність рятує життя, як у медицині з вимірюванням судин.
Практичні приклади використання формул
У будівництві діаметр кола визначає розмір арок чи труб, забезпечуючи стабільність. Наприклад, в архітектурі Пантеону в Римі діаметр купола – 43.3 метри – став еталоном для інженерів. У сучасному світі, за даними з сайту mathros.net.ua, діаметр колеса автомобіля впливає на швидкість і витрату пального.
Інший приклад – астрономія: діаметр Місяця, близько 3474 км, дозволяє розрахувати його видиму величину з Землі. А в спорті, як у баскетболі, діаметр обруча – 45.7 см – диктує правила гри. Ці ілюстрації показують, як абстрактна формула стає частиною нашого щоденного досвіду.
Застосування діаметра кола в реальному житті
Діаметр кола пронизує технології, від мікроскопічних чіпів до гігантських телескопів. У медицині, наприклад, діаметр кровоносних судин вимірюється для діагностики, де навіть міліметр може вказати на проблему. Уявіть хірурга, що планує операцію: точний діаметр аорти – ключ до успіху.
У транспорті діаметр коліс поїздів визначає сумісність з рейками, а в авіації – розмір пропелерів для оптимальної тяги. За даними з 79000.com.ua, в 2025 році діаметр сонячних панелей на супутниках оптимізується для максимальної ефективності. Ці застосування роблять діаметр не просто математичним поняттям, а інструментом прогресу.
Навіть у мистецтві, як у картинах да Вінчі, пропорції кіл базуються на діаметрах, створюючи гармонію. А в екології діаметр деревних стовбурів допомагає оцінювати вік лісів, впливаючи на політику збереження.
Діаметр у науці та техніці
У фізиці діаметр частинок у квантовій механіці визначає взаємодії, тоді як у техніці – розмір антен для сигналу. Приклад: діаметр Великого адронного колайдера – 27 км – дозволяє прискорювати частинки до швидкостей світла. Ці масштаби надихають, показуючи, як проста лінія стає основою для відкриттів.
Цікаві факти про діаметр кола
- 🌍 Діаметр Землі на екваторі – 12 756 км, але на полюсах він менший на 43 км через сплюснутість, що робить нашу планету не ідеальним колом, а еліпсоїдом.
- 🔭 Найбільший телескоп світу у 2025 році, ELT, має дзеркало діаметром 39 метрів, дозволяючи бачити галактики на відстані мільярдів років.
- 🍕 Стандартний діаметр піци – 30 см, але в Італії традиційні – 32 см, що впливає на порції та культурні звички.
- 🕰 У годинниках діаметр циферблата еволюціонував від 5 см у кишенькових до 40 см у настінних, відображаючи зміни в дизайні.
- 🚀 Діаметр ракети SpaceX Starship – 9 метрів – робить її однією з найбільших, дозволяючи нести вантаж до Марса.
Ці факти додають шарму математиці, перетворюючи сухі цифри на історії, що захоплюють уяву. Вони показують, як діаметр кола переплітається з людським досвідом, від космосу до кухні.
Типові помилки при роботі з діаметром кола
Одна з поширених помилок – плутанина діаметра з хордою: не кожна лінія через коло є діаметром, якщо вона не проходить через центр. Це призводить до помилок у розрахунках, як у шкільних задачах, де учні забувають подвоїти радіус. Інша пастка – ігнорування одиниць вимірювання, коли діаметр у сантиметрах змішується з метрами, спотворюючи результати.
У програмуванні алгоритми для малювання кіл можуть ігнорувати точність діаметра, призводячи до спотворених зображень. А в інженерії недооцінка діаметра труб може спричинити витоки. Уникнення цих помилок вимагає уваги до деталей, роблячи геометрію дисципліною точності.
| Аспект | Діаметр | Радіус | Застосування |
|---|---|---|---|
| Визначення | Лінія через центр | Від центру до краю | Розрахунок ширини |
| Формула | d = 2r | r = d/2 | Площа, окружність |
| Приклад | 10 см (колесо) | 5 см | Автомобільні шини |
| Помилка | Плутанина з хордою | Забуття множення | Неправильні масштаби |
Ця таблиця ілюструє ключові відмінності, базуючись на даних з освітніх ресурсів як miyklas.com.ua. Вона допомагає візуалізувати, чому точність у діаметрі критична для практичних задач.
Поради для початківців у вивченні діаметра кола
Починайте з простих малюнків: візьміть циркуль, намалюйте коло і проведіть діаметр – відчуйте його симетрію руками. Потім експериментуйте з формулами, обчислюючи діаметр знайомих об’єктів, як тарілки чи м’яча. Це перетворює теорію на особистий досвід, роблячи навчання захоплюючим.
Використовуйте онлайн-інструменти 2025 року, як симулятори на освітніх платформах, для візуалізації змін діаметра. І не бійтеся помилок – вони найкращі вчителі, особливо коли ви порівнюєте розрахунки з реальними вимірами. З часом діаметр кола стане вашим союзником у розумінні світу геометрії.
Для просунутих: занурюйтесь у неевклідову геометрію, де діаметр поводиться інакше на сферах, відкриваючи нові горизонти. Ці поради, натхненні реальними уроками, роблять вивчення не обов’язком, а пригодою.