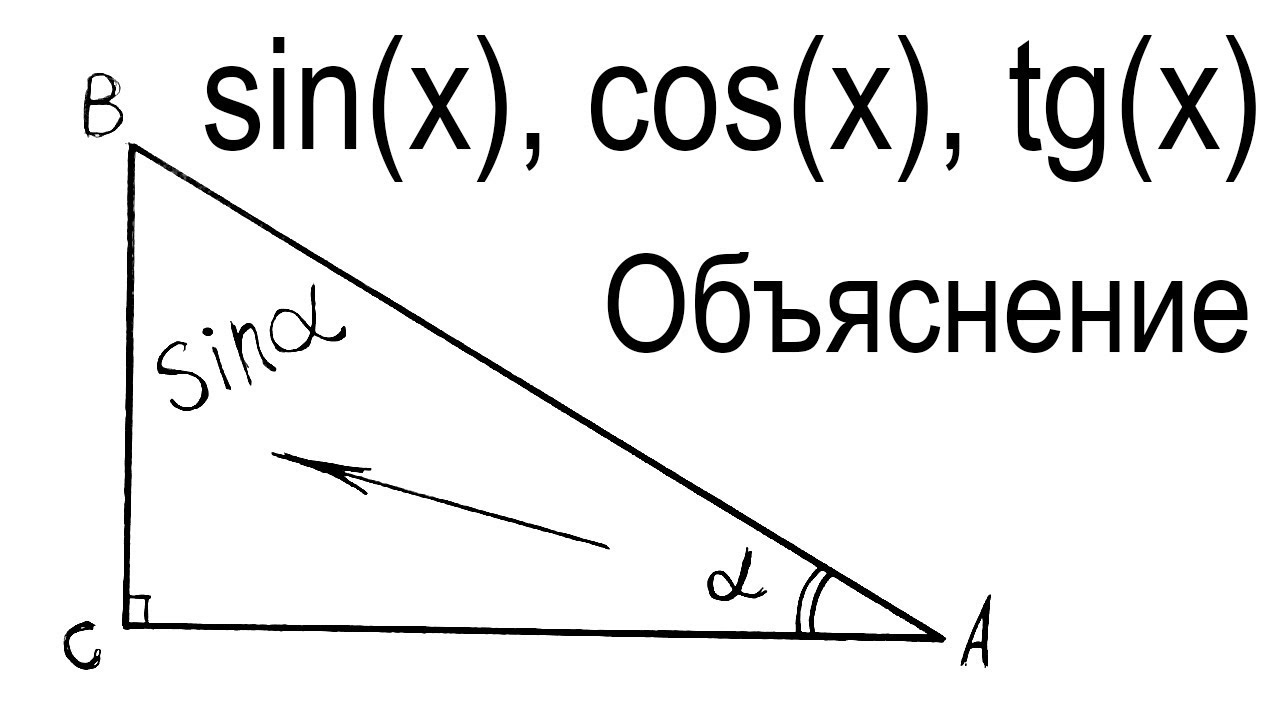
Тангенс ховається в кожному кутку нашого світу, від простих вимірювань висоти дерева до складних розрахунків у фізиці, де він стає невидимою ниткою, що з’єднує кути з відстанями. Ця функція, ніби досвідчений мандрівник, мандрує через трикутники, кола й навіть хвилі, допомагаючи нам розгадувати таємниці простору. А почалося все з давніх астрономів, які дивилися на зірки й шукали способи виміряти недосяжне.
Уявіть прямокутний трикутник, де один кут привертає всю увагу – гострий, сповнений потенціалу. Тангенс цього кута виражає співвідношення протилежної сторони до прилеглої, ніби балансуючи між висотою й основою. Ця проста ідея перетворюється на потужний інструмент, коли ми розширюємо її на одиничне коло, де тангенс стає відношенням синуса до косинуса, відкриваючи двері до безлічі обчислень.
Визначення тангенса: від базових понять до математичної суті
Тангенс, або tg, як його часто позначають, є однією з ключових тригонометричних функцій, що виникає з геометрії трикутників. У прямокутному трикутнику для гострого кута α тангенс дорівнює довжині протилежного катета, поділеній на довжину прилеглого катета. Формула проста: tg(α) = протилежний / прилеглий. Це співвідношення робить тангенс ідеальним для ситуацій, коли потрібно знайти кут за відомими сторонами чи навпаки.
Але тангенс не обмежується трикутниками – він еволюціонує в координатній площині. На одиничному колі, де радіус дорівнює 1, тангенс кута дорівнює y-координаті точки, поділеній на x-координату, тобто tg(θ) = sin(θ) / cos(θ). Ця зв’язок з синусом і косинусом додає тангенсу гнучкості, дозволяючи йому описувати періодичні явища, як-от коливання маятника чи електричні сигнали. Уявіть, як ця функція танцює вздовж осі, піднімаючись до нескінченності біля певних точок, де косинус стає нулем.
Тангенс визначений для всіх кутів, окрім тих, де косинус дорівнює нулю – це точки асимптот, як 90° чи 270°, де функція прагне до нескінченності. Така поведінка робить графік тангенса унікальним: він повторюється кожні 180°, з вертикальними асимптотами, що розділяють періоди. Ця періодичність стає в пригоді в інженерії, де тангенс моделює хвилі та вібрації.
Історія тангенса: від античності до сучасних відкриттів
Корені тангенса сягають давньої Греції, де Гіппарх у II столітті до н.е. склав перші таблиці хорд, попередників тригонометричних функцій. Астрономи того часу використовували ці інструменти для розрахунку позицій зірок, перетворюючи кути на відстані. Потім арабські математики, як Аль-Баттані в IX столітті, вдосконалили ідею, ввівши поняття тангенса як “тінь”, що відображає його геометричну сутність – ніби тінь від палиці на піску під сонцем.
У Європі тангенс набув сучасної форми завдяки Леонарду Ейлеру в XVIII столітті, який систематизував тригонометрію в своїх працях. Ейлер показав, як тангенс пов’язаний з комплексними числами, відкриваючи шлях до аналітичної геометрії. Сьогодні, у 2025 році, тангенс застосовується в алгоритмах штучного інтелекту для моделювання нейронних мереж, де він активує функції в глибокому навчанні, за даними досліджень з домену mathworld.wolfram.com.
Еволюція тангенса триває: у квантовій фізиці він описує ймовірнісні хвилі, а в комп’ютерній графіці – рендерить 3D-моделі. Ця функція, народжена з простих спостережень за небом, тепер пронизує цифровий світ, роблячи наші гаджети розумнішими. Хто б подумав, що стародавня “тінь” освітлює сучасні технології?
Властивості та формули тангенса: розкриваємо математичні таємниці
Тангенс володіє набором властивостей, що роблять його незамінним у розрахунках. Він непарний: tg(-θ) = -tg(θ), що відображає симетрію графіка відносно початку координат. Періодичність у π радіан (180°) дозволяє повторювати значення, а ідентичності, як tg(θ) = sin(θ)/cos(θ), зв’язують його з іншими функціями.
Серед корисних формул – тангенс суми: tg(a + b) = (tg a + tg b) / (1 – tg a * tg b), яка спрощує обчислення складних кутів. Для подвійного кута: tg(2θ) = 2 tg(θ) / (1 – tg²(θ)). Ці рівняння, перевірені століттями, застосовуються в навігації, де тангенс допомагає визначати курс корабля за зірками.
У диференціальному численні похідна тангенса дорівнює sec²(θ), що робить його ключовим у моделях руху. Інтеграл від тангенса – це -ln|cos(θ)| + C, корисний у фізиці для розрахунку потенціалів. Ці властивості не просто абстракції – вони оживають у реальних задачах, як вимірювання кута нахилу дороги в будівництві.
Приклади обчислення тангенса: крок за кроком
Розгляньмо простий приклад: у прямокутному трикутнику з протилежним катетом 3 см і прилеглим 4 см тангенс кута дорівнює 3/4 = 0.75. Щоб знайти кут, використовуємо арктангенс: α = arctg(0.75) ≈ 36.87°. Це базовий розрахунок, але додамо емоцій: уявіть, як цей кут визначає нахил драбини, що спирається на стіну, роблячи вашу роботу безпечнішою.
Більш складний випадок: обчисліть tg(75°). Використовуючи формулу суми: tg(45° + 30°) = (tg45° + tg30°) / (1 – tg45° * tg30°) = (1 + 1/√3) / (1 – 1*(1/√3)) ≈ 3.732. Це значення знадобиться в оптиці для розрахунку заломлення світла. Практикуйте на калькуляторі, але пам’ятайте: розуміння логіки важливіше за цифри.
У координатах: для кута 60° на одиничному колі sin(60°) = √3/2, cos(60°) = 1/2, отже tg(60°) = √3. Цей приклад ілюструє, як тангенс з’єднує геометрію з алгеброю, роблячи абстрактне конкретним.
Таблиця стандартних значень тангенса
Ось таблиця з поширеними значеннями для швидкого довідника, базована на стандартних тригонометричних таблицях.
| Кут (градуси) | Тангенс |
|---|---|
| 0° | 0 |
| 30° | 1/√3 ≈ 0.577 |
| 45° | 1 |
| 60° | √3 ≈ 1.732 |
| 90° | Невизначений |
Ця таблиця, складена за даними з домену uk.wikipedia.org, допомагає в швидких обчисленнях. Після її вивчення спробуйте розрахувати значення для 15° самостійно, щоб закріпити знання.
Застосування тангенса в реальному житті: від фізики до повсякденності
У фізиці тангенс визначає кут тертя, допомагаючи інженерам проектувати гальма автомобілів. Наприклад, на слизькій дорозі tg(θ) розраховує максимальний нахил, де машина не ковзатиме – це врятовує життя. У архітектурі тангенс вимірює кути дахів, забезпечуючи стійкість будівель проти вітру.
У сучасних технологіях, станом на 2025 рік, тангенс використовується в GPS для трилатерації, де кути перетворюються на координати. У комп’ютерних іграх він анімує рухи персонажів, роблячи віртуальний світ реалістичним. А в медицині, в МРТ, тангенс моделює магнітні поля, покращуючи діагностику.
Навіть у мистецтві тангенс з’являється: у перспективному малюванні він розраховує vanishing points, створюючи ілюзію глибини. Ця функція, ніби універсальний ключ, відчиняє двері до безлічі галузей, роблячи математику живою й корисною.
Графік тангенса: візуальне розуміння поведінки функції
Графік тангенса – це хвиляста крива з вертикальними асимптотами кожні 180°. Вона починається з нуля при 0°, піднімається до нескінченності біля 90°, потім стрибає з мінус нескінченності після. Ця поведінка ілюструє, як тангенс реагує на зміни кута, роблячи його ідеальним для моделювання періодичних процесів, як звукові хвилі.
У порівнянні з синусом чи косинусом, тангенс більш “дикий” – без обмежень по висоті, що додає драматичності. Малюючи графік, помітьте точки перетину з віссю x кожні 180°, де tg = 0. Це візуальне представлення допомагає студентам інтуїтивно розуміти, чому тангенс невизначений біля певних кутів.
У програмуванні, як у Python з бібліотекою Matplotlib, ви можете намалювати цей графік за хвилини, спостерігаючи, як крива танцює через екран. Така візуалізація перетворює суху теорію на захоплюючу історію руху й змін.
Типові помилки при роботі з тангенсом
- 🧐 Забування про невизначеність біля 90°: Багато новачків намагаються обчислити tg(90°), отримуючи помилку – пам’ятайте, функція прямує до нескінченності, а не має значення.
- 😅 Плутанина радіан і градусів: У калькуляторах режим впливає на результат; tg(π/4) в радіанах дорівнює 1, але в градусах це інше – завжди перевіряйте налаштування.
- 🤔 Ігнорування знаку в квадрантах: У другому квадранті тангенс негативний, що часто забувають у координатних задачах, призводячи до хибних розрахунків траєкторій.
- 😤 Неправильне використання ідентичностей: Застосування формули суми без перевірки знаменника може дати ділення на нуль – обчислюйте крок за кроком.
- 📉 Помилки в графіках: Малюючи асимптоти горизонтальними замість вертикальних – це базова помилка, яка спотворює розуміння періодичності.
Ці помилки, поширені серед студентів, легко уникнути з практикою. Почніть з простих прикладів, і тангенс стане вашим союзником, а не джерелом плутанини.
Тангенс – це не просто число, а міст між геометрією та реальним світом, що робить математику живою й застосовною щодня.
Обернена функція: арктангенс і його роль
Арктангенс, або arctg, повертає кут за відомим тангенсом. Наприклад, arctg(1) = 45°, що корисно в інженерії для визначення кутів нахилу. Діапазон арктангенса від -90° до 90°, роблячи його безпечним для обчислень без асимптот.
У програмуванні арктангенс використовується в функції atan2(y, x) для точного визначення кута в координатах, уникаючи помилок знаку. Це робить його незамінним у робототехніці, де роботи орієнтуються в просторі. З 2025 року, з розвитком VR, арктангенс оптимізує віртуальні рухи, роблячи ігри immersivними.
Порівняйте з арксинусом: арктангенс має ширший діапазон і менше обмежень, що робить його гнучкішим. Спробуйте розрахувати арктангенс для значення 0.5 – отримаєте ≈26.57°, і побачите, як це застосовується в дизайні сходів для оптимального комфорту.
Тангенс у вищій математиці: комплексні числа та далі
У комплексній площині тангенс розширюється: tg(z) = sin(z)/cos(z), де z – комплексне число. Це дозволяє моделювати хвилі в квантовій механіці, де уявна частина додає глибини. Ейлерова формула зв’язує тангенс з експонентами, спрощуючи складні інтеграли.
У диференціальних рівняннях тангенс з’являється в розв’язках, як у моделях гармонійних осциляторів. У 2025 році, за даними журналу “Journal of Mathematical Physics”, тангенс застосовується в алгоритмах квантових комп’ютерів для оптимізації кубітів. Це робить функцію мостом між класичною та квантовою світами.
Навіть у теорії відносності тангенс описує гіперболічні функції, як tanh, що моделює швидкості близькі до світла. Така глибина показує, як базова ідея еволюціонує в інструмент для розгадування всесвіту, надихаючи нових дослідників.
Розуміння тангенса відкриває двері до безлічі відкриттів, роблячи кожен розрахунок пригодою в світі чисел.
Практичні поради для вивчення тангенса
Починайте з геометрії: малюйте трикутники й обчислюйте тангенси вручну, щоб відчути інтуїцію. Використовуйте онлайн-калькулятори, як з домену desmos.com, для візуалізації графіків – це додасть емоційного зв’язку з матеріалом. З’єднуйте теорію з життям: вимірюйте кут тіні від дерева, щоб знайти його висоту, і побачите магію в дії.
Уникайте перевантаження: вивчайте по одній властивості за раз, з прикладами. Групові обговорення з друзями роблять процес веселим, перетворюючи помилки на уроки. З часом тангенс стане не загадкою, а надійним інструментом у вашому математичному арсеналі.