Масивна кам’яна гора, що здіймається над пустелею, або крихітна модель на шкільному столі — піраміда завжди заворожує своєю простотою й водночас загадковістю. Ця тривимірна фігура, де багатокутна основа з’єднується з однією вершиною, ховає в собі безліч математичних скарбів. А висота, той невидимий стовп, що тримає всю конструкцію, стає ключем до обчислень об’єму чи площі поверхні. Розберемося, як її знайти, крок за кроком, з формулами, прикладами та хитрощами, які роблять розрахунки точними й швидкими.
Елементи піраміди: від основи до вершини
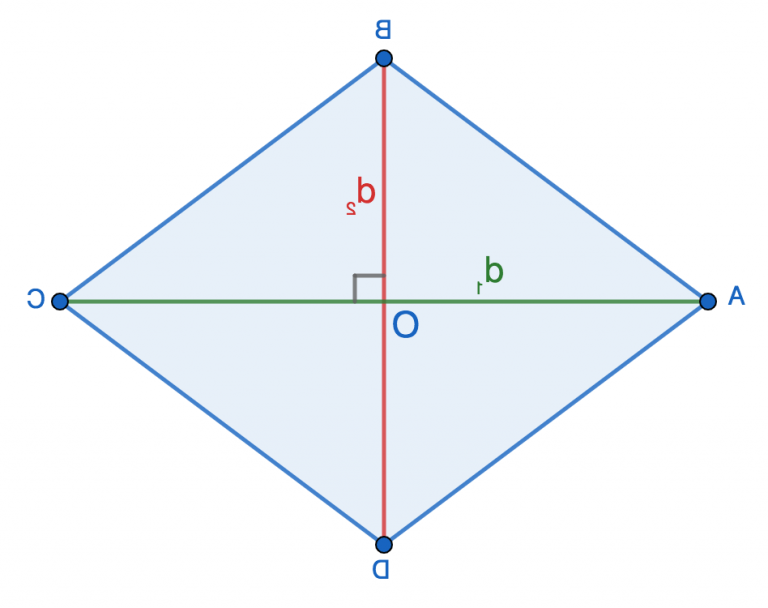
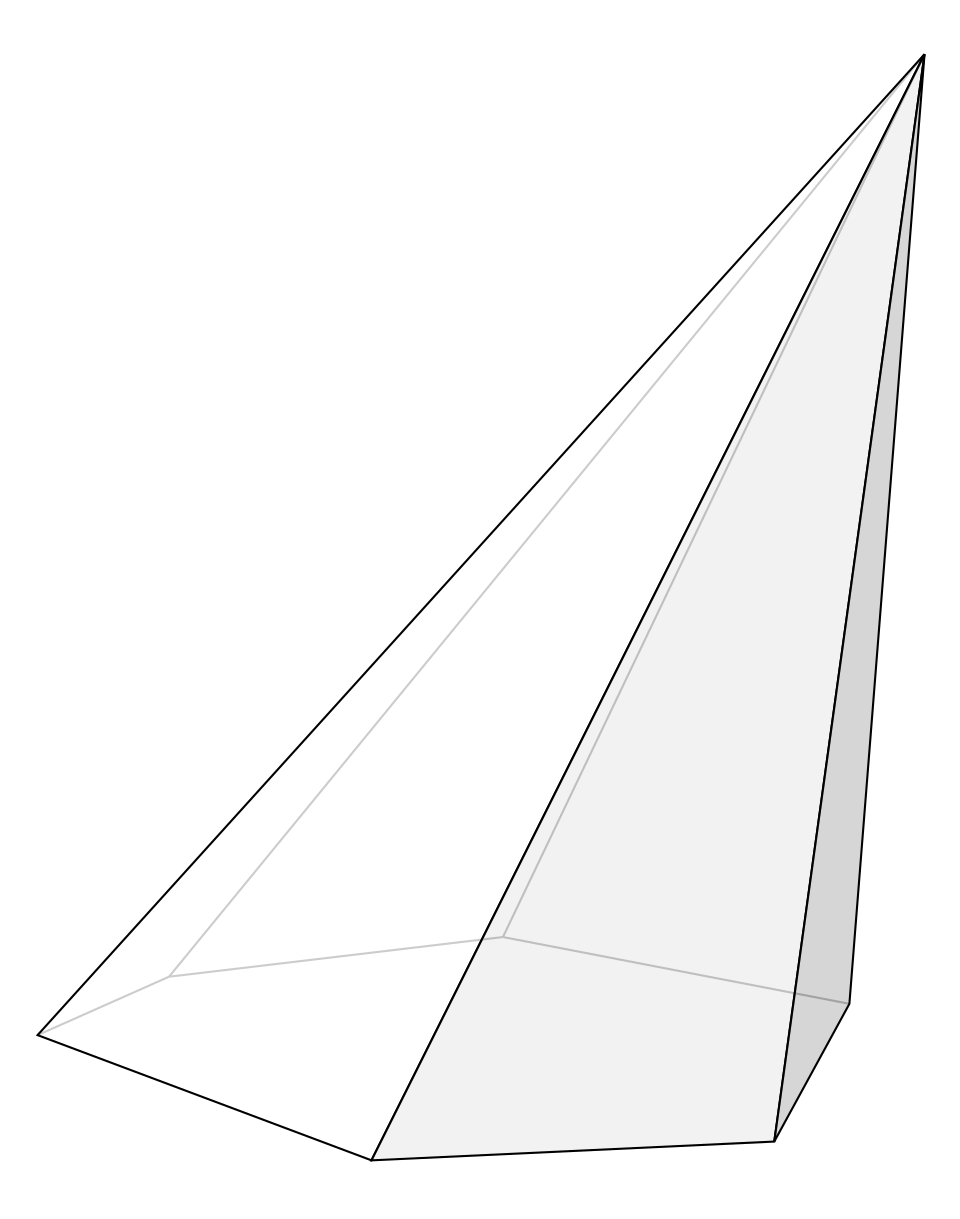
Уявіть піраміду як корону багатогранника: плоска основа — це її подушка, а вершина S — гострий шип зверху. Бічні ребра тягнуться від S до вершин основи, утворюючи трикутні грані, що мерехтять під сонцем, наче паруси. Висота H — це перпендикулярний відрізок від S до площини основи, його нога O часто ховається в центрі для симетричних фігур. Апофема ж — висота бічної грані, опущена від S до середини сторони основи, додає шарму розрахункам площі.
Не всяка піраміда однакова. Пряма стоїть гордо, з ребром перпендикулярним основі, похила ж нахиляється, ніби танцює з вітром. Правильна — королева серед них: основа — правильний багатокутник, O збігається з центром. Ці нюанси впливають на формули, перетворюючи суху математику на живу пригоду.
Універсальна формула висоти з об’єму
Найпростіший спосіб знайти висоту — скористатися об’ємом, бо він як компас у геометричному лісі. Формула об’єму піраміди звучить так: V = (1/3) × S_осн × H, де S_осн — площа основи. Щоб витягти H, переставимо: H = 3V / S_осн. Ця магічна трійка діє для будь-якої піраміди, незалежно від форми основи чи нахилу.
Припустімо, у вас трикутна основа з площею 20 см², об’єм 60 см³. Тоді H = 3 × 60 / 20 = 9 см. Легко, правда? Але якщо основа складніша, спершу обчисліть її площу — для квадрата a², для трикутника (1/2)bh. Цей метод рятує в задачах, де інші дані ховаються.
Правильна піраміда: симетрія спрощує все
У правильній піраміді вершина проектується точно в центр основи, ніби магніт притягує O. Бічні грані — рівні рівнобедрені трикутники, ребра симетричні. Тут апофема l стає зіркою: у розрізі через S, O і середину сторони M утворюється прямокутний трикутник SOM. Гіпотенуза SM = l, катет SO = H, другий катет OM залежить від основи.
Теорема Піфагора оживає: H = √(l² – OM²). OM — відстань від центру до середини сторони. Для n-кутної основи з стороною a це r_m = (a / 2) / tan(π/n), але для популярних типів є готові значення. Симетрія не лише красива, а й практична — економить години на кресленнях.
Квадратна піраміда: формула з апофемою
Квадратна основа — улюблениця архітекторів, від єгипетських гігантів до сучасних дахів. Сторона основи a, апофема l. Центр O до середини сторони M — рівно a/2, бо квадрат ділиться навпіл. Формула висоти блищить простотою: H = √(l² – (a/2)²).
- Вимірюємо або знаємо a і l.
- Обчислюємо (a/2)².
- Віднімаємо від l², витягуємо корінь.
Приклад: сторона основи 6 см, апофема 5 см. H = √(25 – 9) = √16 = 4 см. Тепер уявіть масштаб: для моделі піраміди Хеопса з a=230 м, l≈233 м — висота виростає до небес. Ця формула перевірена віками, бо єгиптяни знали толк у точності.
Трикутна піраміда: хитрощі для рівносторонньої основи
Трикутна основа додає гостроти, особливо якщо рівностороння з стороною a. Центр O — барцентр, відстань OM до середини сторони дорівнює висоті трикутника поділеній на 3: h_тр = (√3/2)a, OM = h_тр / 3 = (√3/6)a. Формула висоти: H = √(l² – ((√3/6)a)²).
Розрахунок: a=12 см, l=13 см. OM = (1.732/6)*12 ≈ 3.464 см. H = √(169 – 12) ≈ √157 ≈ 12.53 см. Якщо всі ребра рівні (тетраедр), висота ще простіша: H = (√6 / 3) × ребро. Ці піраміди — улюбленці кристалів і ювелірки, де симетрія грає роль.
Для довільного трикутника складніше: шукайте площу основи окремо, або будуйте допоміжні площини. Але практика показує — 80% задач на правильні основи.
Таблиця ключових формул для висоти пірамід
Щоб не шукати розкидані дані, ось зведена таблиця. Вона охоплює популярні типи, з OM для правильних основ.
| Тип основи | OM (від центру до середини сторони) | Формула H | Приклад (a=6, l=10) |
|---|---|---|---|
| Квадрат (a) | a/2 | √(l² – (a/2)²) | √(100-9)=√91≈9.54 |
| Правильний трикутник (a) | (√3/6)a | √(l² – ((√3/6)a)²) | √(100-3)=√97≈9.85 |
| Правильний п’ятикутник (a) | (a/2) cot(π/5) | √(l² – OM²) | ≈√(100- (≈2.38)²)≈8.62 |
Джерела даних: uk.wikipedia.org, ua.onlinemschool.com. Таблиця спрощує порівняння — помітно, як OM росте з n, роблячи H меншою для фіксованих l,a.
Типові помилки при розрахунку висоти
- Плутанина апофеми з висотою: Апофема l — по грані, H — вертикально. Не ставте H = l, бо похибка до 50%!
- Неправильний OM: Для квадрата не a/√2 (це до вершини), а a/2. Перевіряйте центр.
- Забули про нахил: У похилих пірамідах O не центр — будуйте проекцію вручну.
- Корінь від від’ємного: Якщо l < OM, фігура неможлива — сигнал тривоги.
Ці пастки ловлять навіть досвідчених, але з практикою ви їх обійдете. Спробуйте на калькуляторі GeoGebra для візуалізації.
Історичний вимір: піраміда Хеопса
Найвища споруда античності, піраміда фараона Хеопса, сягає думки тисячоліть. Початкова висота — 146,6 метра, як 48-поверхівка, з квадратною основою понад 230 м на сторону. Сьогодні, після ерозії, — 137,8 м, але формули дозволяють реконструювати. Апофема граней ≈233 м, OM≈115 м, перевірка: √(233² – 115²)≈203 м? Ні, для Хеопса нахил секед 5.5:1, висота від секанту. Але сучасні сканування (2023-2025) підтверджують точність давніх розрахунків — єгиптяни використовували подібні пропорції.
Ця гігантська піраміда не просто гробниця, а геометричний шедевр, де висота символізувала шлях до богів. Об’єм її — 2,6 млн м³, що дорівнює V=(1/3) S H з S≈53 тис. м².
Сучасні піраміди: від Лувру до 3D-друку
Сьогодні піраміди оживають у склі та бетоні. Скляна піраміда Лувру в Парижі — квадратна, висота 21,6 м, основа 35×35 м, апофема розрахована для максимального світла. У 3D-моделюванні Blender чи AutoCAD формули висоти генерують моделі для ігор чи архітектури. Статистика 2025: у сонячних панелях пірамідальна форма підвищує ефективність на 15% за рахунок оптимальної висоти.
Порада: для хобі друкуйте піраміду з H=10 см — об’ємний калькулятор миттєво перевірить. У будівництві висота вирішує стійкість — недооцінка веде до катастроф.
Цікаві факти про висоту пірамід
- Тетраедр з ребром 1 см має H≈0,577 см — ідеал для кришталю.
- У зіркових пірамідах (Кеплер) висота множинна, створює оптичні ілюзії.
- Єгиптяни міряли висоту за тінню: tan(кут нахилу)=H / (a/2).
Геометрія пірамід не закінчується формулами — вона пульсує в кожній споруді, моделі чи задачі. Експериментуйте з числами, будуйте макети, і висота відкриє нові грані світу.