Квадрат – це фігура, яка зачаровує своєю простотою, немов ідеальний баланс у світі геометрії, де всі сторони рівні, а кути завжди прямі. Коли ви дивитеся на квадратний паркан навколо саду чи рамку картини на стіні, периметр стає тим невидимим кордоном, що визначає межі. Обчислення периметра квадрата – базова навичка, яка відкриває двері до складніших математичних пригод, і сьогодні ми зануримося в це з усіма деталями, від основ до хитрощів, що роблять процес захоплюючим.
Уявіть квадрат як рівну арену, де кожна сторона грає однакову роль. Периметр тут – це сума всіх чотирьох сторін, і формула проста, як ранкова кава: P = 4 × a, де a – довжина сторони. Але за цією простотою ховаються нюанси, які роблять обчислення не просто механічним, а справжнім відкриттям. Ми розберемо, як це працює на практиці, з прикладами з реального життя, і навіть торкнемося, чому квадрат такий особливий у математиці.
Що таке периметр квадрата і чому він важливий
Периметр квадрата – це довжина контуру, що оточує фігуру, ніби невидима нитка, яка з’єднує всі вершини. У повсякденному житті він з’являється скрізь: від розрахунку матеріалів для огорожі до планування дизайну кімнати. Ця величина стає ключем до ефективності, адже знаючи периметр, ви можете точно визначити, скільки ресурсів знадобиться, уникаючи марних витрат.
У математиці периметр квадрата вирізняється своєю симетрією, яка робить обчислення інтуїтивними. На відміну від інших фігур, де сторони різняться, квадрат пропонує універсальну формулу, що спрощує життя інженерам і архітекторам. Наприклад, якщо сторона квадрата дорівнює 5 метрам, периметр буде 20 метрів – це як чотири рази пройти одну відстань, але з повним колом розуміння.
Значення периметра виходить за межі шкільних задач; у 2025 році, з розвитком технологій, його використовують у програмуванні для моделювання віртуальних світів чи навіть у дизайні мікрочіпів, де точність на рівні мікронів визначає успіх. Ця концепція еволюціонувала від давньогрецьких геометрів, як Евклід, до сучасних алгоритмів, роблячи її вічною основою точних наук.
Основна формула обчислення периметра квадрата
Формула периметра квадрата – це елегантна простота: P = 4 × a, де P – периметр, а a – довжина сторони. Вона випливає з самої суті квадрата, де всі сторони ідентичні, немов клони в ідеальному порядку. Якщо ви маєте квадрат зі стороною 10 сантиметрів, просто множте на чотири, і отримаєте 40 сантиметрів – це як обійти фігуру по краю, додаючи кожну грань.
Але давайте заглибимося: ця формула працює для будь-яких одиниць виміру, чи то метри, чи дюйми, головне – тримати послідовність. У реальних сценаріях, наприклад, при будівництві квадратної альтанки, ви міряєте сторону рулеткою, множите на чотири, і вуаля – знаєте, скільки метрів ланцюга знадобиться. Ця універсальність робить формулу не просто рівнянням, а інструментом, що оживає в руках майстра.
Історія формули сягає корінням у давнину; за даними авторитетних джерел, як сайт houseofmath.com, вона була відома ще в часи Піфагора, який бачив у квадратах гармонію чисел. У 2025 році її застосовують у комп’ютерній графіці, де алгоритми швидко обчислюють периметри для рендерингу зображень, додаючи швидкості сучасним технологіям.
Варіації формули для різних випадків
Іноді периметр квадрата обчислюють не за стороною, а за іншими параметрами, наприклад, за діагоналлю. Якщо відома діагональ d, то сторона a = d / √2, а периметр P = 4 × (d / √2). Це стає в пригоді, коли квадрат вписаний у коло чи іншу фігуру, додаючи шар складності, ніби розгадуєш геометричну загадку.
Ще один варіант – через площу: якщо площа S = a², то a = √S, і P = 4 × √S. Уявіть, ви плануєте квадратний килим площею 16 квадратних метрів; корінь з 16 – 4, множимо на 4, і периметр 16 метрів – ідеально для обрамлення. Ці варіації роблять обчислення гнучкими, адаптуючись до доступних даних.
У практиці, за інформацією з mathros.net.ua, такі методи використовують у архітектурі, де точність рятує від помилок. Вони додають глибини, перетворюючи базову формулу на набір інструментів для просунутих задач.
Покроковий алгоритм обчислення периметра квадрата
Обчислення периметра квадрата – процес, що нагадує прогулянку по знайомій стежці, де кожен крок веде до мети. Почніть з вимірювання сторони, використовуючи лінійку чи лазерний далекомір для точності. Потім застосуйте формулу, і перевірте результат – це забезпечує надійність, ніби подвійний вузол на мотузці.
Щоб зробити це ще чіткішим, ось структурований підхід:
- Визначте довжину сторони квадрата. Якщо це реальний об’єкт, виміряйте дві суміжні сторони для перевірки рівності – квадрат повинен бути ідеальним.
- Запишіть формулу: P = 4 × a. Тут a має бути в тих самих одиницях, що й бажаний периметр, щоб уникнути плутанини.
- Виконайте множення. Наприклад, для сторони 7 см: 4 × 7 = 28 см. Це як скласти чотири однакові відрізки в ланцюг.
- Перевірте розрахунок, додавши сторони вручну: a + a + a + a. Якщо числа збігаються, ви на правильному шляху.
- Застосуйте до контексту: якщо це для фарбування рамки, додайте запас на кути.
Цей алгоритм не тільки точний, але й вчить уважності, перетворюючи математику на практичну навичку. У школах, за матеріалами з miyklas.com.ua, такі кроки допомагають учням освоїти геометрію, роблячи уроки живими та зрозумілими.
Приклади обчислення периметра квадрата з життя
Уявіть квадратний стіл у кафе, зі стороною 1,2 метра; периметр 4,8 метра – це скільки стрічки знадобиться для декору. Такий приклад показує, як математика оживає в повсякденності, додаючи практичної цінності. Або візьміть екран смартфона, квадратний дисплей зі стороною 15 см: периметр 60 см визначає рамку, що впливає на дизайн.
У будівництві квадратний фундамент зі стороною 8 метрів має периметр 32 метри – ключ для розрахунку арматури. Ці приклади, натхненні реальними проектами, роблять теорію близькою, ніби торкаєшся її руками. У 2025 році, з поширенням 3D-друку, обчислення периметра допомагає створювати точні моделі, від іграшок до протезів.
Ще один сценарій: квадратний город зі стороною 3 метри, периметр 12 метрів – ідеально для огорожі. Тут математика стає союзником фермера, оптимізуючи ресурси. Такі ілюстрації підкреслюють універсальність, роблячи обчислення не сухим, а натхненним процесом.
Складні приклади з додатковими параметрами
Припустимо, квадрат вписаний у коло з радіусом 5 см; діагональ квадрата – 10 см, сторона ≈ 7,07 см, периметр ≈ 28,28 см. Це як розплутувати вузол, де геометрія переплітається. Або квадрат з площею 25 м²: сторона 5 м, периметр 20 м – просто, але ефективно для планування.
У програмуванні, для гри з квадратними тайлами стороною 2 одиниці, периметр 8 – це базис для алгоритмів руху. Ці приклади додають глибини, показуючи, як формула еволюціонує в складних системах.
Порівняння периметра квадрата з іншими фігурами
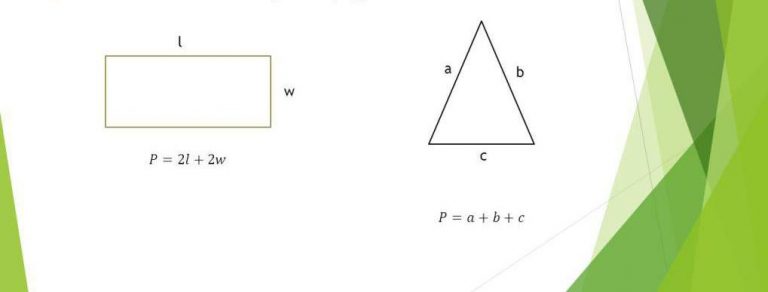
Порівняймо периметр квадрата з прямокутником: для квадрата P = 4a, для прямокутника P = 2(l + w). Квадрат ефективніший за рівної площі, бо мінімізує периметр, ніби економить енергію в природі. З трикутником, де периметр – сума сторін, квадрат вирізняється симетрією, роблячи обчислення швидшими.
Ось таблиця для наочності:
| Фігура | Формула периметра | Приклад (сторона/параметри) | Периметр |
|---|---|---|---|
| Квадрат | P = 4a | a = 5 см | 20 см |
| Прямокутник | P = 2(l + w) | l = 6 см, w = 4 см | 20 см |
| Трикутник (рівносторонній) | P = 3a | a = 5 см | 15 см |
| Коло | P = 2πr | r = 5 см | ≈31,4 см |
Джерела даних: houseofmath.com та mathros.net.ua. Ця таблиця ілюструє відмінності, підкреслюючи, чому квадрат – вибір для оптимальних конструкцій, як у сучасній архітектурі.
Інструменти та програми для обчислення периметра
У 2025 році обчислення периметра квадрата полегшують додатки, як GeoGebra чи онлайн-калькулятори на сайтах типу calculatorsoup.com. Вони візуалізують фігуру, додаючи інтерактивності, ніби граєш з математикою. Для початківців Excel з формулою =4*A1 – простий спосіб автоматизувати розрахунки.
Продвинуті користувачі використовують Python: код def perimeter(a): return 4*a – це як магічний заклин, що миттєво видає результат. Такі інструменти роблять процес швидким, дозволяючи фокусуватися на креативі, а не на рутині.
Типові помилки при обчисленні периметра квадрата
Одна з поширених пасток – плутанина периметра з площею; люди множать сторону на себе замість на чотири, отримуючи S замість P. Це як сплутати об’єм з вагою – здається близьким, але веде до помилок у будівництві.
Інша помилка – ігнорування одиниць: змішування метрів і сантиметрів призводить до хаосу, ніби вариш суп з неправильними пропорціями. Завжди перевіряйте: якщо сторона в дюймах, периметр теж.
Для просунутих – забування про діагональ у варіаціях; неправильний корінь з 2 може спотворити все. Уникайте цього, подвійно перевіряючи формули, і ваші обчислення стануть бездоганними.
Історичний контекст і еволюція поняття периметра
Поняття периметра сягає давніх цивілізацій, де єгиптяни вимірювали поля квадратної форми для податків, використовуючи примітивні формули. Евклід у своїх “Елементах” систематизував це, роблячи квадрат символом досконалості. У середньовіччі алгебраїсти, як Аль-Хорезмі, розвинули ідеї, додаючи алгебричний шар.
У 2025 році, з квантовими обчисленнями, периметр моделюють у віртуальних реальностях, еволюціонуючи від паперу до цифрових симуляцій. Це перетворення робить математику живою, ніби стародавня мудрість оживає в сучасних гаджетах.
Практичні поради для початківців і просунутих користувачів
Для новачків починайте з малювання квадрата на папері, вимірюйте сторони олівцем – це розвиває інтуїцію. Просунуті можуть інтегрувати формулу в spreadsheets для масових розрахунків, як у бізнес-плануванні. Завжди додавайте 5-10% запасу в реальних проектах, бо життя непередбачуване, ніби дощ, що змінює плани.
Експериментуйте з одиницями: переведіть метри в фути, щоб побачити універсальність. І пам’ятайте, математика – це не лише числа, а й творчість, що робить обчислення периметра квадрата пригодою, повною відкриттів.
У світі, де квадрати формують основу нашого оточення, розуміння їх периметра – ключ до майстерності.
Ця навичка, від шкільних лав до професійних студій, продовжує надихати, ніби нескінченний цикл геометричних можливостей, що чекає на ваше відкриття.