Дроби оточують нас скрізь, від рецептів на кухні, де половина склянки борошна може вирішити долю пирога, до складних розрахунків у фізиці, де частки секунди визначають траєкторію руху. Вони ніби маленькі пазли, що складають ціле, і розуміння, як їх порівнювати, відкриває двері до впевненості в математиці. Ця навичка стає мостом між простою арифметикою та глибокими концепціями, дозволяючи бачити числа не як сухі символи, а як живі сутності з власними характерами.
Коли ми беремо два дроби, скажімо 3/4 і 2/3, вони можуть здаватися загадковими, наче два незнайомці на вечірці, яких потрібно представити один одному. Але з правильними методами порівняння все стає прозорим, ніби розкриваєш таємницю за допомогою лупи. Ми розберемо це крок за кроком, починаючи з базових підходів для новачків і переходячи до хитрощів для тих, хто вже відчуває себе комфортно в світі чисел.
Основи порівняння дробів: чому це важливо і як почати
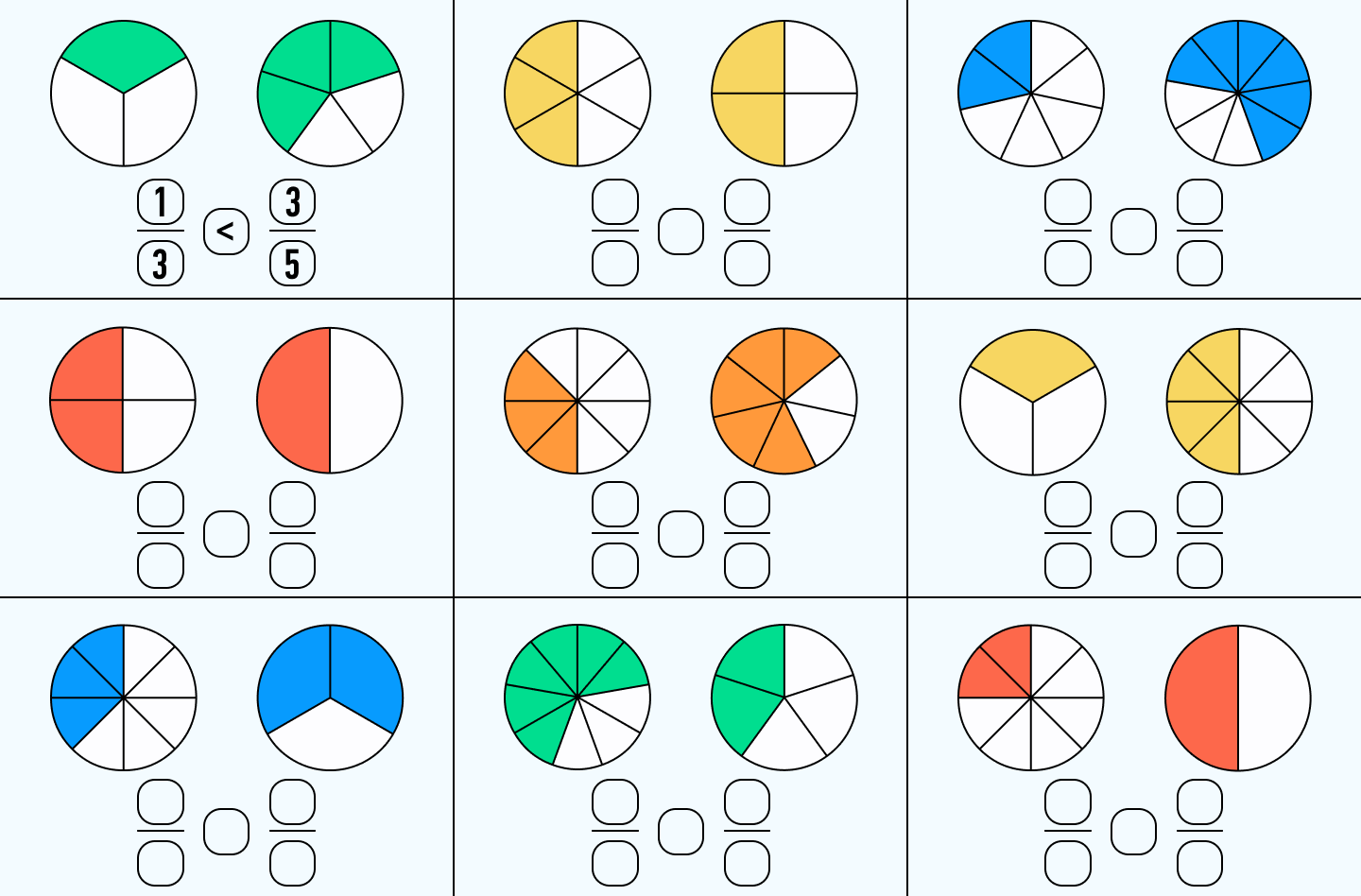
Порівняння дробів – це не просто шкільна вправа, а інструмент, що допомагає в повсякденному житті, наприклад, коли вибираєш кращу знижку в магазині чи розраховуєш пропорції в рецепті. Уявіть, як дріб 1/2 стає половиною яблука, а 3/4 – трьома чвертями піци; зрозуміти, який більший, значить уникнути помилок у розподілі. Для початківців ключ у візуалізації: малюйте кола чи прямокутники, розділені на частини, щоб побачити різницю наочно.
Історично дроби з’явилися тисячі років тому, в Стародавньому Єгипті та Вавилоні, де їх використовували для вимірювання земель і податків, як зазначає Britannica. Ця давня практика еволюціонувала, і сьогодні ми маємо чіткі правила, які роблять порівняння точним і швидким. Почніть з дробів з однаковими знаменниками – тут все просто, як порівняння висот двох дерев за однаковою шкалою: більший чисельник означає більший дріб.
Наприклад, візьміть 2/5 і 3/5; оскільки знаменники рівні, 3/5 явно більший, бо три частини з п’яти перевищують дві. Це базовий крок, що будує впевненість, ніби перший крок дитини, яка вчиться ходити. А тепер додамо емоції: уявіть радість від того, як дитина розуміє, що 4/7 більше за 2/7, бо це ніби більше шматочків улюбленого торта з однакових порцій.
Методи для початківців: прості кроки з прикладами
Для тих, хто тільки знайомиться з дробами, найкращий старт – метод приведення до спільного знаменника. Він діє як універсальний перекладач, що робить різні дроби порівнянними. Візьміть 1/2 і 1/3: спільний знаменник – 6, тож 1/2 стає 3/6, а 1/3 – 2/6. Тепер ясно, що 3/6 > 2/6, ніби порівнюєш дві купки монет після обміну на однакові номінали.
Інший простий спосіб – використання десяткових дробів. Перетворіть 3/4 на 0.75, а 5/8 на 0.625 – і ось, 0.75 більший. Це особливо зручно для новачків, бо десяткові числа знайомі з грошима: 0.75 долара більше за 0.625. Згідно з освітніми ресурсами як Khan Academy, цей метод допомагає візуалізувати через діаграми, роблячи абстрактне конкретним.
А ось приклад з життя: уявіть, ви ділите піцу. Якщо один друг бере 2/5, а інший 3/8, приведіть до спільного знаменника 40: 2/5 = 16/40, 3/8 = 15/40. Так, 16/40 > 15/40, і ви знаєте, хто отримав більше. Ці методи не просто правила – вони інструменти, що додають впевненості, ніби ключі до замка скарбниці знань.
- Визначте, чи знаменники однакові. Якщо так, порівняйте чисельники безпосередньо – більший чисельник виграє.
- Якщо знаменники різні, знайдіть найменше спільне кратне (НСК) для них. Це число стане новим знаменником для обох дробів.
- Перетворіть дроби: помножте чисельник і знаменник кожного на відповідний множник, щоб отримати еквівалентні дроби зі спільним знаменником.
- Порівняйте нові чисельники: той, що більший, вказує на більший дріб.
- Для перевірки використайте візуалізацію, як розділення прямокутника на частини, щоб побачити різницю очима.
Ці кроки роблять процес систематичним, але додають шарму, коли ви застосовуєте їх до реальних ситуацій, як планування бюджету, де 1/4 зарплати на розваги може бути більше чи менше за 3/10 на їжу. З практикою це стає інтуїтивним, ніби їзда на велосипеді після перших невдалих спроб.
Порівняння для просунутих: глибокі методи та нюанси
Коли ви переходите на просунутий рівень, порівняння дробів набуває відтінків стратегії, ніби гра в шахи з числами. Один з потужних методів – перехресне множення, ідеальний для дробів з різними знаменниками. Для 3/5 і 4/7 перемножте 3 на 7 (21) і 4 на 5 (20); оскільки 21 > 20, то 3/5 > 4/7. Це швидкий трюк, що економить час, ніби блискавка в математичному небі.
Для ще глибшого занурення розгляньте порівняння через різницю або відношення. Обчисліть різницю: 3/4 – 2/3 = (9-8)/12 = 1/12, що показує, наскільки один більший. Або використовуйте відношення: розділіть один дріб на інший, якщо результат >1, то перший більший. Ці підходи додають аналітичної глибини, особливо в задачах з фізики чи економіки, де дроби представляють швидкості чи ймовірності.
Просунуті користувачі можуть звернутися до властивостей дробів, як порівняння з одиницею: якщо дріб >1, він більший за будь-який правильний дріб. Наприклад, 5/4 (1.25) явно перевищує 7/8 (0.875). А для негативних дробів пам’ятайте, що -3/4 < -1/2, бо на числовій прямій більша абсолютна величина робить число меншим у негативній зоні. Це додає шарів, ніби відкриваєш нові рівні в грі.
Використання десяткових і відсотків для точності
На просунутому рівні перетворення в десяткові стає не просто зручністю, а інструментом для складних порівнянь. Візьміть ірраціональні дроби, як 1/√2 і 1/√3; обчисліть ≈0.707 і ≈0.577, і ясно, що перший більший. Це особливо корисно в інженерії, де точність до кількох знаків після коми може врятувати проект.
Відсотки додають ще один вимір: 3/5 = 60%, 2/3 ≈66.67%, тож 2/3 більший. У бізнесі це допомагає порівнювати прибутки, ніби зважувати золоті монети на терезах. Згідно з MathWorld, такі перетворення базуються на фундаментальних властивостях чисел, забезпечуючи надійність.
| Дріб 1 | Дріб 2 | Метод | Результат |
|---|---|---|---|
| 3/4 | 5/6 | Спільний знаменник (12) | 9/12 < 10/12, тож 3/4 < 5/6 |
| 2/5 | 3/7 | Перехресне множення | 2*7=14, 3*5=15; 14<15, тож 2/5 < 3/7 |
| 1/3 | 0.4 | Десяткове перетворення | ≈0.333 < 0.4 |
| -1/2 | -3/5 | Порівняння з урахуванням знаку | -0.5 > -0.6 |
Ця таблиця ілюструє різні методи в дії, показуючи їх універсальність. Дані базуються на стандартних математичних правилах, як описано на сайтах naurok.com.ua та childdevelop.com.ua. Вона допомагає візуалізувати, як теорія переходить у практику, додаючи впевненості в розрахунках.
Практичні приклади з життя та математики
Уявіть, ви на кухні: рецепт вимагає 2/3 склянки молока, а у вас є 3/4 – чи вистачить? Порівняйте: 2/3 ≈0.666, 3/4=0.75, тож так, і навіть з лишком. Це робить математику живою, ніби додає спецій до страви. У спорті дроби порівнюють статистику: гравець з 4/5 успішних кидків кращий за того з 5/7? Перехресне: 4*7=28, 5*5=25; 28>25, тож 4/5 > 5/7.
Для просунутих – у фізиці: швидкість 3/4 м/с проти 5/6 м/с. Спільний знаменник 12: 9/12 < 10/12, тож друга більша. А в програмуванні дроби в алгоритмах: порівняння 1/π і 1/e ≈0.318 vs ≈0.367, показує 1/e > 1/π. Ці приклади роблять теорію частиною реальності, ніби з’єднують дроти в електричному ланцюзі.
Типові помилки при порівнянні дробів
- 😩 Ігнорування знаменників: Багато новачків порівнюють лише чисельники, думаючи, що 3/10 > 2/5, бо 3>2, але насправді 3/10=0.3 < 0.4=2/5. Це ніби судити книгу за обкладинкою, не заглядаючи всередину.
- 🤔 Неправильне знаходження НСК: Замість найменшого спільного кратного беруть просто добуток знаменників, що ускладнює обчислення, як для 2/3 і 3/4 – добуток 12, але це і є НСК, та для інших це марнує час.
- 😤 Забуття про знак: При негативних дробах, як -4/5 і -3/4, дехто думає -4/5 менший, але -0.8 < -0.75, тож навпаки. Це пастка, ніби слизька стежка в лісі.
- 🙄 Плутанина з мішаними числами: Порівнюючи 2 1/2 і 2 1/3, забувають перетворити в неправильні: 5/2=2.5 > 7/3≈2.333. Без цього все йде шкереберть.
- 😅 Надмірне спрощення: Скорочуючи перед порівнянням, дехто втрачає еквівалентність, але насправді скорочення не змінює значення, просто робить числа меншими для легкості.
Ці помилки – як камені на шляху, але усвідомлення їх робить вас сильнішим, ніби воїна, що вчиться на поразках. Уникаючи їх, ви перетворюєте порівняння на мистецтво, повне відкриттів.
Розширені техніки: від теорії до застосування
Для справжніх ентузіастів є методи на основі нерівностей, як правило Баттерфлая: для позитивних a/b і c/d, якщо a/b > c/d, то (a+c)/(b+d) лежить між ними. Це корисно в аналізі, ніби мереживо, що з’єднує дроби в складні візерунки. У статистиці порівняння дробів допомагає в ймовірностях: 2/5 ймовірність дощу проти 3/7 – перехресне показує 2/5 < 3/7, тож готуйте парасольку.
Історичний нюанс: Евклід у “Початках” описував порівняння через евклідів алгоритм для НСК, що досі актуально. Сучасні додатки, як у комп’ютерних моделях, використовують дроби для графіки, де порівняння визначає пікселі. Це робить тему вічною, ніби ріка, що тече крізь століття.
Наостанок, експериментуйте з дробами в іграх: створіть гру, де порівняння визначає переможця, додаючи веселощів. Чи в мистецтві, де пропорції – це дроби, як золотий перетин ≈1.618, що перевищує 3/2=1.5. Так математика стає частиною творчості, розкриваючи безмежні горизонти.