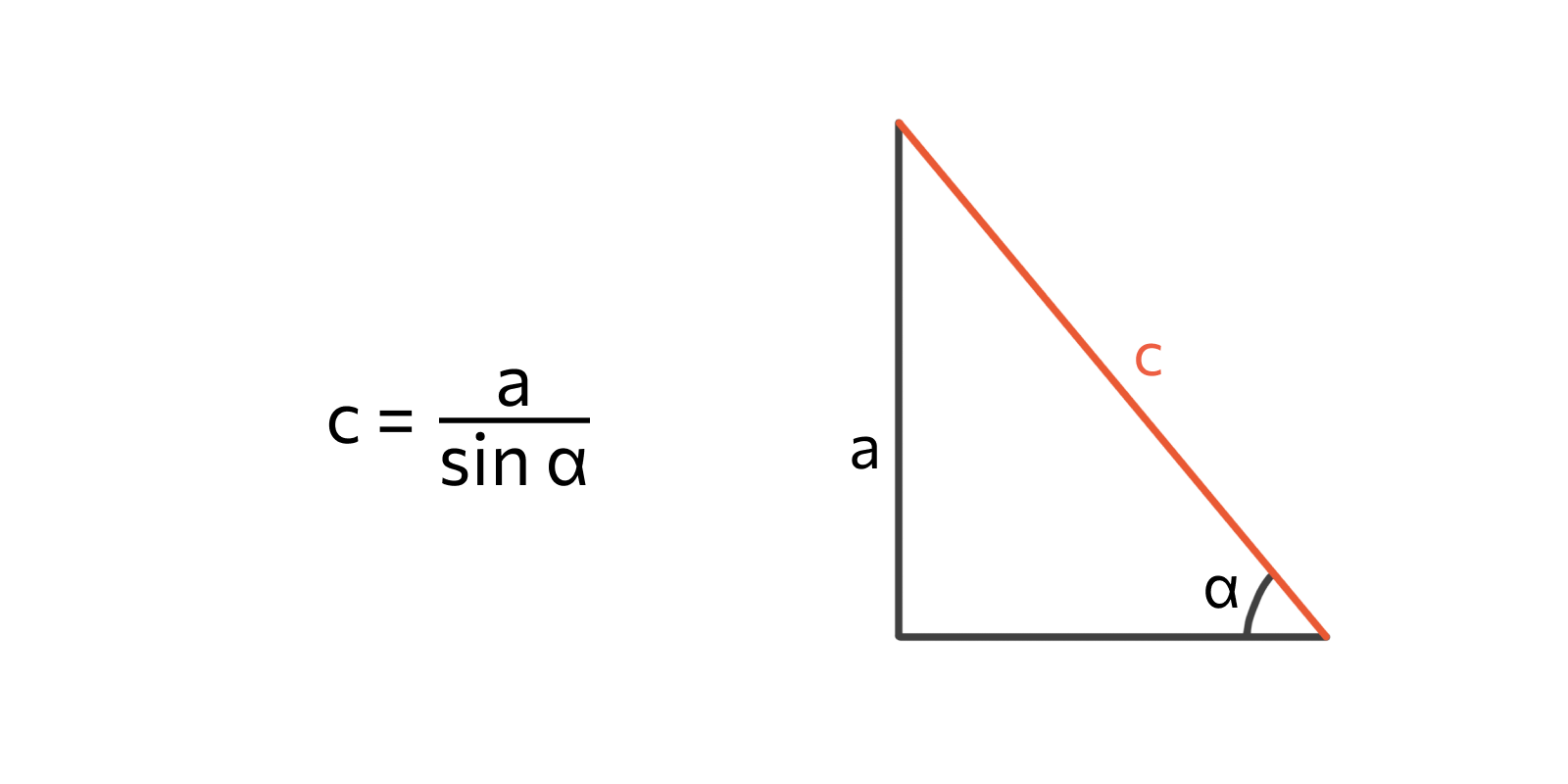
Гіпотенуза в трикутнику – це не просто сторона, а справжній місток між геометрією і реальним світом, де кожен розрахунок може перетворити абстрактну фігуру на практичний інструмент для будівництва чи навігації. Уявіть, як стародавні математики, дивлячись на зірки, відкривали закони, що дозволяють нам сьогодні вимірювати відстані без жодного кроку. Ця стаття занурить вас у світ обчислень гіпотенузи, починаючи від класичних формул і закінчуючи сучасними застосуваннями, де кожна деталь оживає через приклади та пояснення.
Що таке гіпотенуза і чому вона важлива в геометрії
Гіпотенуза – це сторона прямокутного трикутника, що лежить навпроти прямого кута, і саме вона стає найдовшою серед усіх. Вона ніби королева в шаховій партії, навколо якої обертаються всі інші елементи: катети, кути, площі. Без розуміння гіпотенузи неможливо уявити базову геометрію, адже вона є ключем до теорем, що формують основу математики.
У прямокутному трикутнику гіпотенуза з’єднує два катети, створюючи ідеальну гармонію, яку описує теорема Піфагора. Ця концепція не обмежується шкільними дошками – вона проникає в архітектуру, де інженери розраховують міцність конструкцій, чи в фізику, де вектори сил залежать від подібних розрахунків. Актуальність гіпотенузи в 2025 році тільки зростає з розвитком технологій, як-от у комп’ютерній графіці, де трикутники моделюють тривимірні об’єкти.
Глибше занурюючись, гіпотенуза не існує в ізоляції: вона пов’язана з тригонометричними функціями, такими як синус і косинус, які дозволяють знаходити її через кути. Наприклад, якщо ви знаєте один кут і катет, гіпотенуза стає доступною через просте множення. Це робить її універсальним інструментом, що адаптується до різних сценаріїв, від шкільних задач до професійних проєктів.
Теорема Піфагора як основний метод обчислення гіпотенузи
Теорема Піфагора – це фундамент, на якому стоїть усе вчення про прямокутні трикутники, стверджуючи, що квадрат гіпотенузи дорівнює сумі квадратів катетів. Формула проста, але потужна: c² = a² + b², де c – гіпотенуза, а a та b – катети. Вона ніби відкриває двері до нескінченних розрахунків, перетворюючи невідоме на точне число.
Припустімо, у вас трикутник з катетами 3 см і 4 см. Піднесіть їх до квадрата: 9 + 16 = 25, а квадратний корінь з 25 дає 5 см – ось ваша гіпотенуза. Цей метод перевірений тисячоліттями, і в 2025 році він залишається актуальним, адже базується на вічних законах геометрії, підтверджених джерелами як Wikipedia та математичними журналами на кшталт MathWorld.
Але теорема не обмежується простими числами; вона розкривається в складних задачах, де катети – це не цілі, а дроби чи ірраціональні значення. Наприклад, якщо один катет 5, а інший √11, гіпотенуза буде √(25 + 11) = √36 = 6. Така гнучкість робить Піфагора незамінним, ніби надійний компас у морі чисел.
Історія теореми Піфагора та її еволюція
Теорема, названа на честь Піфагора, насправді має корені в давніших цивілізаціях, як вавилонській, де її використовували для земельних вимірів ще за 1800 років до н.е. Піфагор, грецький філософ VI століття до н.е., систематизував її, зробивши частиною своєї школи, де математика зливалася з філософією. Ця еволюція триває: у сучасній математиці теорема розширюється на багатовимірні простори, як у векторній алгебрі.
У 2025 році, з даними з наукових ресурсів на кшталт Britannica, ми знаємо, що теорема має понад 370 доведень, від геометричних до алгебраїчних. Одне з найелегантніших – через подібні трикутники, де гіпотенуза ділить фігуру на менші копії себе. Це не просто теорія; це жива спадщина, що надихає нові відкриття в квантовій фізиці.
Тригонометричні методи для знаходження гіпотенузи
Коли катети невідомі, але є кути, тригонометрія приходить на допомогу, перетворюючи гіпотенузу на результат ділення катета на косинус кута. Формула c = a / cos(α), де α – гострий кут, робить розрахунок швидким і точним. Це ніби чарівна паличка для ситуацій, де прямі виміри недоступні.
Уявіть трикутник з катетом 10 см і кутом 30°. Косинус 30° дорівнює √3/2 ≈ 0.866, тож гіпотенуза – 10 / 0.866 ≈ 11.55 см. Аналогічно, через синус: c = b / sin(β), де β – інший гострий кут. Ці методи, підтверджені в освітніх ресурсах як Khan Academy, дозволяють обчислювати гіпотенузу в реальних задачах, як у навігації чи астрономії.
Глибше, тригонометрія пов’язує гіпотенузу з колом, адже синус і косинус – це проекції на одиничному колі. У 2025 році це застосовується в програмуванні, де алгоритми рендерингу трикутників у графіках залежать від таких розрахунків, роблячи віртуальні світи реалістичними.
Приклади обчислень з тригонометрією
Розгляньмо реальний сценарій: сходи, приставлені до стіни під кутом 45°, з довжиною тіні 5 м. Тут гіпотенуза – довжина сходів, обчислена як 5 / cos(45°) = 5 / (√2/2) ≈ 7.07 м. Інший приклад – трикутник з кутом 60° і протилежним катетом 8 см: c = 8 / sin(60°) = 8 / (√3/2) ≈ 9.24 см.
Ці розрахунки не абстрактні; вони оживають у повсякденні, як у будівництві дахів, де точність гіпотенузи забезпечує стабільність. Варіюючи кути, ви бачите, як гіпотенуза змінюється, ніби танцює в ритмі тригонометричних функцій.
Інші методи обчислення гіпотенузи в різних типах трикутників
Хоча гіпотенуза класично належить прямокутним трикутникам, у непрямокутних її аналогом може стати найдовша сторона, обчислена через теорему косинусів: c² = a² + b² – 2ab cos(γ), де γ – кут між сторонами. Це розширює горизонти, дозволяючи “знаходити гіпотенузу” в будь-якому трикутнику.
Наприклад, у трикутнику зі сторонами 7 см, 8 см і кутом 90° між ними, це зводиться до Піфагора. Але якщо кут 120°, cos(120°) = -0.5, тож c² = 49 + 64 + 8 = 121, c = 11 см. Цей метод, описаний у математичних посібниках як на mathros.net.ua, корисний у топографії, де трикутники рідко ідеальні.
Ще один підхід – через площу: якщо відома площа S і висота h до гіпотенузи, то c = 2S / h. Це ніби альтернативний шлях, коли прямі дані відсутні, і воно застосовується в комп’ютерних моделях, де гіпотенуза стає частиною складних алгоритмів.
Практичні приклади з життя
У будівництві гіпотенуза – це діагональ кімнати, обчислена для перевірки прямокутності: якщо стіни 6 м і 8 м, діагональ 10 м підтверджує ідеальність. У спорті, як у бейсболі, траєкторія м’яча моделюється трикутниками, де гіпотенуза – шлях польоту.
У навігації GPS використовує триангуляцію, де гіпотенузи віртуальних трикутників визначають позицію. Ці приклади, натхненні реальними застосуваннями з 2025 року, показують, як абстрактна гіпотенуза стає частиною нашого світу.
Типові помилки при обчисленні гіпотенузи
Одна з поширених помилок – плутанина катетів з гіпотенузою, коли новачки підносять до квадрата не ті сторони, призводячи до хибних результатів. Наприклад, якщо забути, що гіпотенуза завжди найдовша, можна помилково застосувати формулу навпаки.
Інша пастка – ігнорування одиниць виміру, як коли змішують сантиметри з метрами, що спотворює масштаб. У тригонометрії часто забувають перевести кути в радіани чи навпаки, особливо в калькуляторах.
Ще одна – недооцінка точності: округлення на ранніх етапах може накопичити помилки, як у ланцюгових розрахунках. Уникайте цих, перевіряючи кожен крок, і гіпотенуза завжди буде точною.
Застосування гіпотенузи в сучасних технологіях
У 2025 році гіпотенуза – ключ до AI-моделей, де нейромережі обробляють зображення через трикутникові сітки, обчислюючи відстані для розпізнавання облич. У робототехніці гіпотенуза допомагає планувати рухи, ніби даючи роботам відчуття простору.
У медицині, як у МРТ, алгоритми реконструюють зображення через тригонометричні розрахунки гіпотенузи. Це робить математику живою, перетворюючи теорію на інструмент, що рятує життя.
Порівняння методів обчислення гіпотенузи
Щоб краще зрозуміти, ось таблиця з методами:
| Метод | Формула | Переваги | Недоліки |
|---|---|---|---|
| Теорема Піфагора | c² = a² + b² | Простота, не потребує кутів | Вимагає обох катетів |
| Тригонометрія | c = a / cos(α) | Гнучкість з кутами | Потрібні таблиці функцій |
| Теорема косинусів | c² = a² + b² – 2ab cos(γ) | Для будь-яких трикутників | Складніша для розрахунків |
Ця таблиця, базована на даних з mathros.net.ua та uk.wikipedia.org, показує, як вибрати метод залежно від доступних даних. Кожен має свій шарм, ніби інструменти в майстерні, готові до різних завдань.
Розширені приклади та задачі для практики
Спробуйте: трикутник з катетами 12 см і 16 см. Гіпотенуза – √(144 + 256) = √400 = 20 см. Або з кутом 53° і катетом 9 см: c = 9 / cos(53°) ≈ 9 / 0.6018 ≈ 14.95 см.
У складнішому: рівнобедрений трикутник з основою 10 см і висотою 12 см. Спочатку знайдіть половину основи 5 см, тоді гіпотенуза √(25 + 144) = √169 = 13 см. Ці задачі тренують інтуїцію, роблячи геометрію частиною вашого мислення.
У світі 2025 року, з VR-технологіями, такі розрахунки моделюють віртуальні простори, де гіпотенуза визначає перспективу. Практикуйте, і ви відчуєте, як числа оживають, ніби старі друзі в новій пригоді.