Об’єм – це той невидимий простір, який заповнює кожну річ навколо нас, від крихітної краплі води до величезного океану. Коли ви тримаєте в руках склянку, наповнену соком, ви відчуваєте її вагу, але саме об’єм визначає, скільки рідини поміститься всередині. Ця концепція пронизує наше життя, від будівництва будинків до приготування їжі, і розуміння, як знайти об’єм, відкриває двері до точних розрахунків у математиці, фізиці та повсякденних справах. Уявіть, як архітектори моделюють кімнати, щоб вони були зручними, або як інженери обчислюють місткість резервуарів – все це починається з базових формул об’єму. А тепер зануримося глибше, розкриваючи, як ці розрахунки еволюціонували від давніх часів до сучасних застосувань.
Історія концепції об’єму: від давнини до сучасності
Уявіть стародавніх єгиптян, які будували піраміди, не маючи сучасних калькуляторів, але інтуїтивно розуміючи, скільки каменю потрібно для заповнення простору. Концепція об’єму сягає корінням у часи Архімеда, який, за легендою, вигукнув “Еврика!” у ванні, відкривши принцип витіснення рідини для вимірювання об’єму неправильних тіл. Цей момент став поворотним: об’єм перестав бути абстракцією і перетворився на інструмент для наукових відкриттів. У середньовіччі математики як Евклід систематизували формули для геометричних тіл, заклавши основу для сучасної геометрії. Сьогодні, з появою комп’ютерного моделювання, обчислення об’єму стало ще точнішим, дозволяючи симулювати складні структури в 3D-програмах. Наприклад, у медицині томографи розраховують об’єм органів, допомагаючи діагностувати хвороби з неймовірною точністю. Ця еволюція показує, як проста ідея перетворилася на фундаментальний елемент науки.
Але історія не обмежується теорією. У 17 столітті Кавальєрі розвинув принцип, який дозволяє порівнювати об’єми через перерізи, що нагадує нарізання пирога на шматочки для оцінки загальної порції. Цей метод став основою для інтегрального числення, яке ми використовуємо сьогодні для складних форм. У реальному житті це застосовується в автомобільній промисловості, де дизайнери обчислюють об’єм двигуна, щоб оптимізувати паливну ефективність. Без розуміння цих історичних кроків ми б не мали інструментів для сучасних інновацій, як-от 3D-друк, де об’єм визначає кількість матеріалу для створення об’єктів. Тож, вивчаючи, як знайти об’єм, ми торкаємося спадщини геніїв минулого.
Основні принципи обчислення об’єму: базові поняття
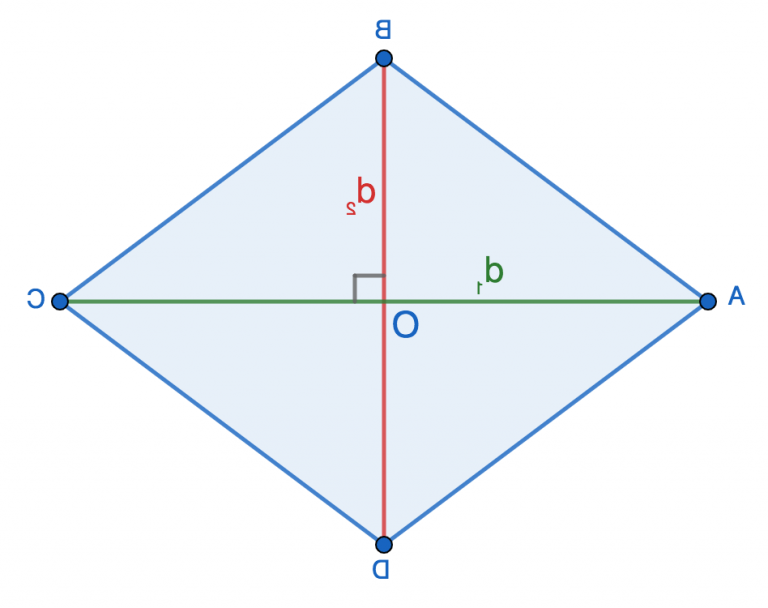
Об’єм вимірюється в кубічних одиницях, як кубічні метри або сантиметри, що відображає тривимірну природу простору. Щоб знайти об’єм, ми множимо довжину, ширину та висоту для прямокутних форм, але для криволінійних тіл це стає справжнім викликом, вимагаючи формул, що враховують кривизну. Подумайте про куб: його об’єм – це просто сторона в кубі, але за цим стоїть ідея заповнення простору ідентичними одиницями. У фізиці об’єм пов’язаний з густиною, де маса ділиться на об’єм, даючи розуміння матеріалу. Ці принципи роблять розрахунки універсальними, від шкільних задач до інженерних проєктів.
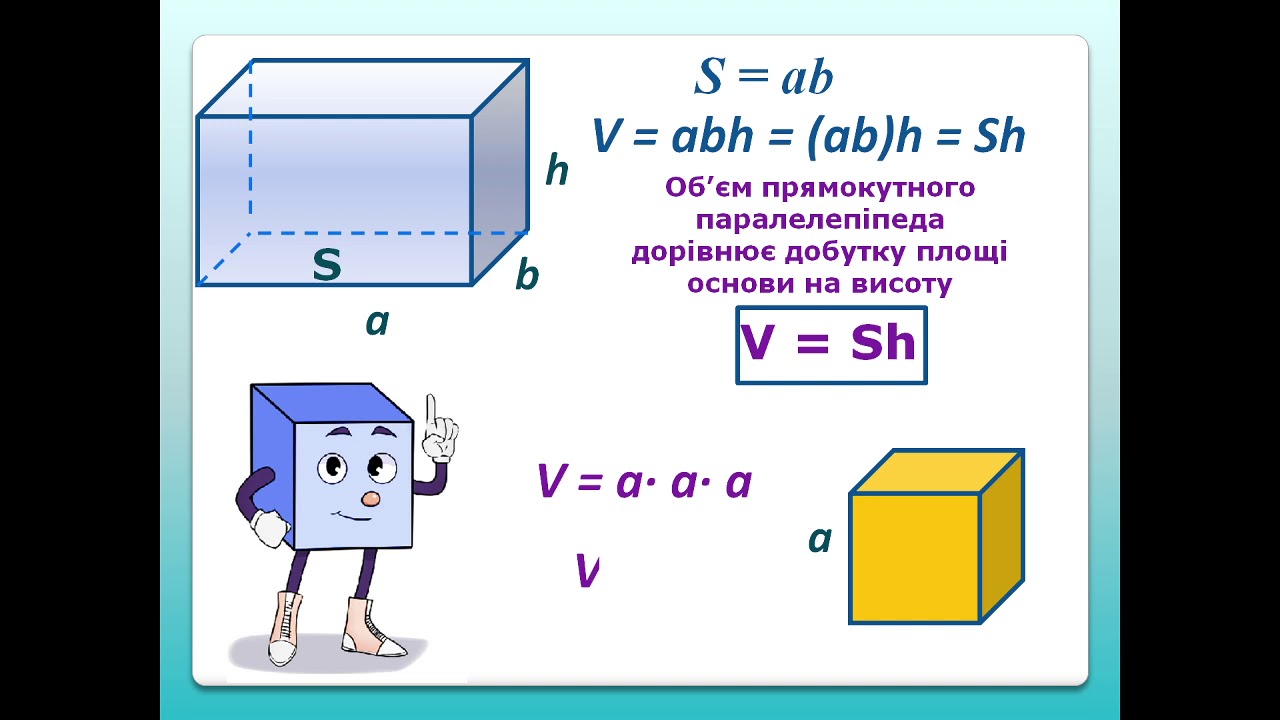
Одним з ключових інструментів є формула для призм: об’єм дорівнює площі основи, помноженій на висоту. Це працює для будь-якої призми, чи то трикутної, чи шестикутної, роблячи метод гнучким. Для пірамід формула подібна, але з коефіцієнтом 1/3, що відображає звуження форми до вершини. Ці базові ідеї дозволяють розбирати складні об’єкти на простіші частини, як пазл, де кожен шматочок додає до загальної картини. У практиці це означає, що інженер, проектуючи міст, може розрахувати об’єм бетону, уникаючи перевитрат. Розуміння цих принципів робить математику не сухою теорією, а живими інструментами для творчості.
Об’єм прямокутного паралелепіпеда та куба
Прямокутний паралелепіпед – це як коробка з чіткими гранями, де об’єм обчислюється за формулою V = l × w × h, де l – довжина, w – ширина, h – висота. Ця простота обманлива: у реальних задачах вимірювання цих параметрів вимагає точності, бо навіть міліметр може змінити результат. Наприклад, для шафи розмірами 2 м на 1 м на 0.5 м об’єм складе 1 кубічний метр, ідеально для планування простору в кімнаті. Куб – спеціальний випадок, де всі сторони рівні, тож V = a³, і це формула, яку діти вивчають першою, бо вона інтуїтивна, як будівництво з кубиків Lego.
У будівництві ця формула застосовується для розрахунку об’єму фундаментів, де помилка може призвести до катастрофи. А в кулінарії, коли ви печете торт у прямокутній формі, знання об’єму допомагає точно дозувати інгредієнти. Ці приклади показують, як базова математика стає частиною повсякденності, додаючи впевненості в діях.
Об’єм призм і циліндрів
Для призм об’єм – це площа основи помножена на висоту, V = S × h. Якщо основа – трикутник з площею 10 см² і висота 5 см, то об’єм 50 см³. Циліндр, як призма з круглою основою, має формулу V = π r² h, де r – радіус, h – висота. Уявіть банку з консервованими овочами: її об’єм визначає, скільки продукту поміститься, і це критично для харчової промисловості.
Ці формули еволюціонували від робіт Архімеда, який вивчав циліндри в контексті сфер. Сьогодні в гідравліці об’єм циліндрів розраховують для систем гальмування в автомобілях, забезпечуючи безпеку. Розуміння цих розрахунків дозволяє уникнути помилок, як переповнення контейнерів, і робить життя ефективнішим.
Об’єм пірамід, конусів і сфер: складніші форми
Піраміда з її звуженою формою має об’єм V = (1/3) S h, де S – площа основи, h – висота. Для піраміди Хеопса об’єм становить приблизно 2,5 мільйона кубічних метрів, що ілюструє грандіозність давніх споруд. Конус подібний, V = (1/3) π r² h, і це формула для морозива в ріжку, де об’єм визначає порцію. Сфера, найсиметричніше тіло, має V = (4/3) π r³, і її об’єм розраховують для планет, як Земля з радіусом близько 6371 км.
Ці формули вимагають точних вимірювань, бо для сфер навіть невелика похибка в радіусі кубічно впливає на результат. У медицині об’єм сфероподібних клітин вивчають для розуміння біологічних процесів, а в астрономії – для оцінки зірок. Ці приклади додають глибини, показуючи, як математика переплітається з природою.
Методи для неправильних тіл
Для неправильних форм, як камінь, використовують метод витіснення: помістіть об’єкт у воду і виміряйте підйом рівня. Це принцип Архімеда в дії, де зміна об’єму рідини дорівнює об’єму тіла. У сучасних технологіях 3D-сканери обчислюють об’єм через інтеграли, розділяючи об’єкт на крихітні шматочки.
У промисловості це застосовують для моделювання прототипів, де програмне забезпечення як AutoCAD інтегрує формули для точних розрахунків. Ці методи роблять обчислення доступними навіть для складних форм, перетворюючи хаос на порядок.
Практичні приклади розрахунку об’єму в реальному житті
Уявіть, ви плануєте басейн: для прямокутного з розмірами 10 м × 5 м × 2 м об’єм 100 м³, що означає 100 000 літрів води. Це допомагає оцінити витрати на наповнення. У фармацевтиці об’єм пігулок розраховують для дозування ліків, забезпечуючи ефективність.
Ще приклад – розрахунок об’єму паливного бака в автомобілі: циліндричний бак з радіусом 0.3 м і висотою 1 м має об’єм близько 0.28 м³, або 280 літрів. Такі розрахунки економлять час і ресурси, роблячи життя практичнішим.
Перед тим, як зануритися в приклади, ось таблиця з базовими формулами для швидкого огляду.
| Фігура | Формула об’єму | Приклад |
|---|---|---|
| Куб | V = a³ | Для a=2 см: V=8 см³ |
| Циліндр | V = π r² h | Для r=3 см, h=5 см: V≈141.37 см³ |
| Сфера | V = (4/3) π r³ | Для r=4 см: V≈268.08 см³ |
| Піраміда | V = (1/3) S h | Для S=10 см², h=6 см: V=20 см³ |
Ця таблиця ілюструє, як формули застосовуються на практиці, з числовими прикладами для кращого розуміння. Вона підкреслює універсальність обчислень, дозволяючи швидко адаптувати їх до різних сценаріїв.
Застосування об’єму в науці та технологіях
У хімії об’єм газів розраховують за законом Бойля-Маріотта, де тиск і об’єм обернено пропорційні, допомагаючи в експериментах. У екології об’єм лісів оцінюють для моніторингу вирубки, використовуючи супутникові дані. Технології як VR симулюють об’єми віртуальних світів, роблячи ігри immersивними.
У 2025 році, з розвитком AI, програми автоматично обчислюють об’єм для логістики, оптимізуючи вантажі в контейнерах. Це зменшує відходи і підвищує ефективність, показуючи, як математика впливає на глобальну економіку.
Типові помилки при розрахунку об’єму
Розрахунок об’єму здається простим, але помилки чатують на кожному кроці. Ось найпоширеніші, з порадами, як їх уникнути.
- 🚫 Змішування одиниць вимірювання: Якщо довжина в метрах, а ширина в сантиметрах, результат буде хаотичним. Завжди переводьте все в одну систему, як метри, для точності.
- ⚠️ Ігнорування форми основи: Для призм площа основи критична; помилка в розрахунку трикутника призведе до хибного об’єму. Перевіряйте формули для кожної фігури окремо.
- ❌ Неправильне використання π: Округлення π до 3 замість 3.14 спотворює результати для циліндрів. Використовуйте точне значення або калькулятор для прецизності.
- 🔍 Забуття коефіцієнта 1/3 для пірамід: Багато плутають з призмами, множачи повну площу на висоту. Пам’ятайте, піраміда “звужується”, тож діліть на три.
- 📏 Похибки в вимірюваннях: Неточний лінійка дає помилкові дані. Використовуйте цифрові інструменти для реальних проєктів.
Ці помилки часто виникають через поспіх, але усвідомлення їх робить розрахунки надійнішими, перетворюючи новачків на впевнених користувачів.
Розширені методи: інтеграли та комп’ютерне моделювання
Для складних форм, як еліпсоїди, використовують інтегральне числення: об’єм = ∫ π y² dx, де y – функція кривої. Це як нарізання фігури на тонкі диски і сумування їх об’ємів. У програмуванні Python з бібліотекою SymPy дозволяє автоматизувати це, роблячи процес швидким.
У 2025 році AI-інструменти моделюють об’єми в реальному часі, застосовуючи в архітектурі. Це відкриває нові горизонти, де математика зливається з технологіями для інновацій.
А в біології об’єм клітин розраховують для моделювання росту, використовуючи статистичні дані. Точні розрахунки об’єму допомогли в розробці ліків проти раку. Ці методи показують, як глибокі знання перетворюють теорію на практичні рішення.
Об’єм у повсякденному житті: від кухні до подорожей
На кухні об’єм визначає рецепти: для тіста в формі 20×30×5 см об’єм 3 літри, ідеально для великої родини. У подорожах об’єм валіз розраховують, щоб уникнути перевантаження, з формулою для неправильних форм через апроксимацію.
У садівництві об’єм ґрунту для горщиків – ключ до здорових рослин. Ці приклади роблять тему близькою, показуючи, як знайти об’єм стає частиною рутини, додаючи радості в прості речі.