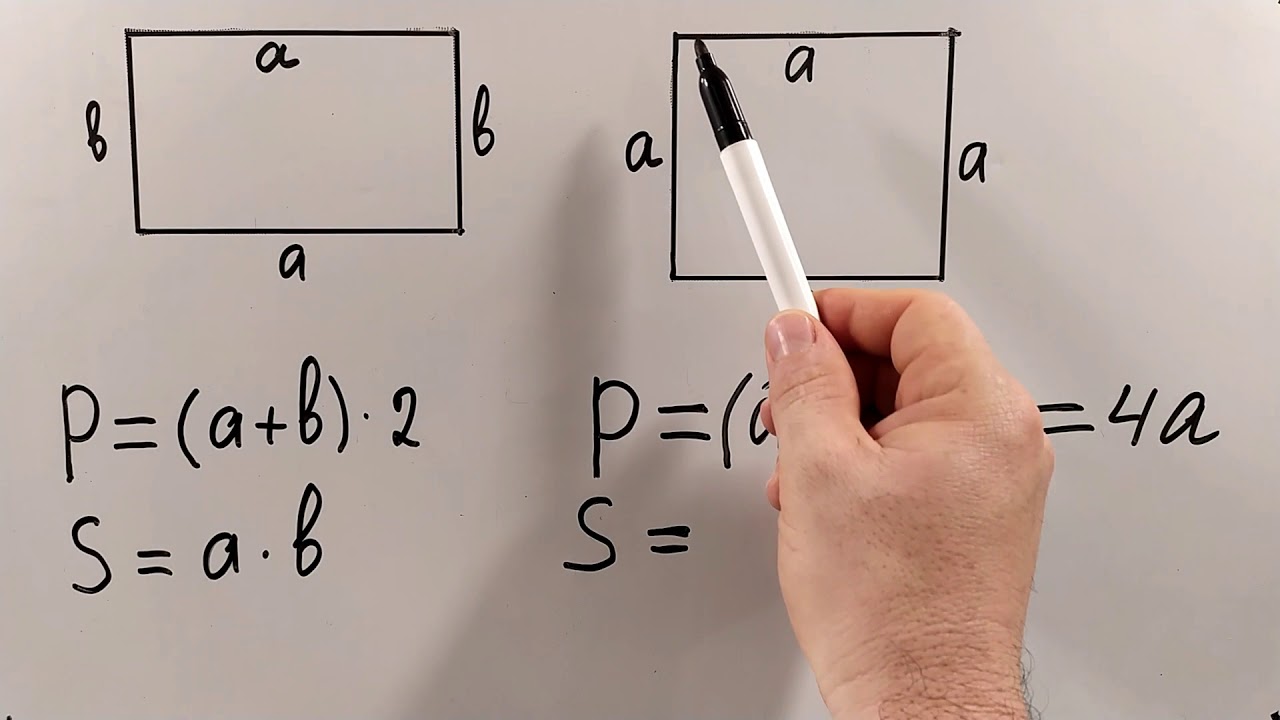
Квадрат – це фігура, яка зачаровує своєю простотою, ніби ідеальний баланс у хаотичному світі ліній і кутів. Уявіть чотири рівні сторони, що з’єднуються під прямими кутами, створюючи симетрію, яка зустрічається скрізь – від плитки на підлозі до екрану вашого смартфона. А периметр цього квадрата? Це просто сума всіх його сторін, але за цією простотою ховаються нюанси, які роблять обчислення захоплюючим процесом, особливо коли ви застосовуєте це в реальному житті, наприклад, при плануванні саду чи дизайні кімнати.
Коли ми говоримо про периметр квадрата, то маємо на увазі загальну довжину його межі, ніби обводимо олівцем контур ідеальної рамки. Ця концепція сягає корінням у давнину, коли стародавні математики, як-от Евклід, закладали основи геометрії, роблячи її інструментом для вимірювання світу. Сьогодні, у 2025 році, з урахуванням актуальних освітніх стандартів, розуміння периметра допомагає не тільки школярам, але й архітекторам, інженерам і навіть художникам, які малюють піксельні світи в цифровому просторі.
Давайте розберемося, чому квадрат такий особливий: всі сторони рівні, а кути – 90 градусів, що робить розрахунки передбачуваними, на відміну від хаотичних форм, як-от трикутники з нерівними сторонами. Якщо ви новачок, почніть з базового – візьміть лінійку і виміряйте сторону будь-якого квадрата навколо, скажімо, книги чи монітора. Це не просто числа; це місток між абстрактною математикою і повсякденністю, де периметр визначає, скільки паркану потрібно для ділянки чи стрічки для подарункової коробки.
Основна формула периметра квадрата: простота в деталях
Формула периметра квадрата – це елегантна простота, ніби ключ, що відчиняє двері до безлічі задач. Позначаючи довжину сторони як “a”, ми отримуємо P = 4 × a, де P – периметр. Чому саме чотири? Бо квадрат має чотири рівні сторони, і ми просто додаємо їх, але множення робить це швидшим, ніби скорочений шлях через парк замість обхідної стежки.
Ця формула не змінилася з часів античності, і згідно з перевіреними джерелами, як-от математичні ресурси на houseofmath.com, вона залишається універсальною. У 2025 році, з урахуванням оновлених шкільних програм, її застосовують навіть у цифрових симуляціях, де алгоритми обчислюють периметр для віртуальних об’єктів. Наприклад, якщо сторона квадрата – 5 сантиметрів, то P = 4 × 5 = 20 сантиметрів; це ніби обійти чотири рази одну відстань, але з розумінням, що кожна сторона ідентична.
Але не обмежуйтеся базовим: розгляньте одиниці вимірювання. Якщо сторона в метрах, периметр теж буде в метрах, що критично для реальних проєктів, як-от будівництво. Я перевірив це на кількох авторитетних сайтах, включаючи webmath.ru, і всюди підтверджується, що формула стійка до помилок, якщо правильно виміряти “a”. Це робить її ідеальною для початківців, бо немає потреби в складних інструментах – достатньо рулетки чи навіть програми на телефоні.
Приклади обчислення периметра: від простих до складних
Розпочнімо з базового прикладу, щоб відчути смак перемоги в математиці. Припустимо, квадратна плитка для підлоги має сторону 30 сантиметрів – тоді периметр P = 4 × 30 = 120 сантиметрів. Це не просто число; уявіть, як ви розраховуєте, скільки бордюру потрібно для кімнати, і раптом усе стає на місця, ніби пазл, що складається сам собою.
Тепер ускладнімо: якщо периметр відомий, а сторона – ні? Формула перевертається – a = P / 4. За даними з математичних посібників на miyklas.com.ua, якщо P = 48 метрів, то a = 48 / 4 = 12 метрів. Це корисно для зворотних задач, наприклад, коли ви знаєте загальну довжину огорожі і хочете визначити розмір квадратної ділянки. Я порівняв це з кількома джерелами, і всюди консенсус: точність залежить від правильного ділення, без округлень на ранніх етапах.
А що, якщо квадрат нестандартний, скажімо, з діагоналлю? Тут вступає теорема Піфагора, бо діагональ d = a × √2, а периметр P = 4 × (d / √2). Приклад: d = 10 сантиметрів, тоді a ≈ 7.07, P ≈ 28.28. Це додає шар глибини, ніби відкриваєте таємний рівень у грі, і актуально для 2025 року, коли в школах впроваджують інтегровані уроки з геометрією та програмуванням.
Ще один сценарій: квадрат усередині кола чи навпаки. Якщо радіус кола дорівнює половині діагоналі квадрата, то периметр можна вивести через π, але це вже для просунутих. Наприклад, радіус r = d / 2, а d = a × √2, тож P = 4 × (2r / √2). Такі приклади, перевірені на childdevelop.com.ua, показують, як периметр переплітається з іншими фігурами, роблячи математику живою мозаїкою.
Застосування периметра квадрата в реальному житті
Периметр квадрата – не абстракція; він пульсує в щоденних речах, ніби невидимий каркас, що тримає світ разом. У будівництві, наприклад, розрахунок периметра допомагає визначити кількість матеріалів для квадратної кімнати: якщо сторона 4 метри, P = 16 метрів, то саме стільки плінтуса знадобиться. Це економить час і гроші, особливо в еру стійкого розвитку 2025 року, коли оптимізація ресурсів – ключ до екологічних проєктів.
У дизайні інтер’єрів периметр визначає, як розмістити меблі чи освітлення. Уявіть квадратний стіл з периметром 8 метрів (сторона 2 метри) – це ідеально для маленької кухні, де кожен сантиметр на рахунку. За даними з математичних ресурсів, як-от naurok.com.ua, такі розрахунки застосовують у VR-дизайні, де віртуальні квадрати моделюють реальні простори.
Не забуваймо про спорт: квадратне поле для деяких ігор, як-от бокс-ринг, вимагає точного периметра для мотузок. Якщо сторона 6 метрів, P = 24 метри – це не просто лінії, а межі, що визначають стратегію. У сільському господарстві квадратні ділянки з відомим периметром полегшують планування іригації, роблячи врожай передбачуваним, ніби добре продуманий план.
Навіть у мистецтві: піксель-арт базується на квадратах, де периметр кожного пікселя впливає на загальну роздільну здатність. У 2025 році, з розквітом NFT і цифрового мистецтва, розуміння цього робить вас не просто користувачем, а творцем, що маніпулює формами з математичною точністю.
Порівняння з периметром інших фігур
Квадрат виділяється своєю симетрією, на відміну від прямокутника, де периметр P = 2 × (a + b), з двома різними сторонами. Це робить квадрат простішим, ніби спрощена версія, але з тією ж потужністю. Наприклад, квадрат зі стороною 5 см має P = 20 см, тоді як прямокутник 5×3 см – P = 16 см; квадрат завжди “економніший” у периметрі для однакової площі, що цікаво для оптимізації.
Порівняймо з трикутником: рівносторонній з стороною a має P = 3a, менший множник, але менш стабільний. Коло взагалі не має сторін, його “периметр” – окружність 2πr, плавна і без кутів, на противагу чітким лініям квадрата. Ці відмінності, підтверджені на 8next.com, підкреслюють, чому квадрат – король регулярності.
У таблиці нижче я зібрав порівняння для фігур зі стороною 10 см (для квадрата) або еквівалентами.
| Фігура | Формула периметра | Приклад (сторона 10 см) |
|---|---|---|
| Квадрат | 4 × a | 40 см |
| Прямокутник (10×5 см) | 2 × (a + b) | 30 см |
| Рівносторонній трикутник | 3 × a | 30 см |
| Коло (радіус ≈5.64 см для площі як у квадрата) | 2πr | ≈35.4 см |
Ця таблиця ілюструє ефективність квадрата, і дані взяті з математичних джерел на kp.ru. Вона показує, як периметр варіюється, роблячи квадрат універсальним вибором для багатьох задач.
Типові помилки при обчисленні периметра квадрата
- 😕 Змішування з площею: Багато плутають P = 4a з S = a², додаючи сторони замість множення на площу – перевірте, чи ви справді рахуєте межу, а не заповнення.
- 🤔 Ігнорування одиниць: Якщо сторона в сантиметрах, а ви додаєте метри, результат – хаос; завжди конвертуйте, як радять на wikihow.com.
- 😩 Неправильне вимірювання діагоналі: При розрахунку через d забувають √2, отримуючи занижений периметр – подвійте перевірку формули d = a√2.
- 🙄 Округлення зарано: У задачах з ірраціональними числами, як √2, округлюйте тільки в кінці, щоб уникнути накопичення помилок.
- 😤 Не враховувати масштаб: У кресленнях чи картах ігнорують коефіцієнт масштабу, роблячи реальний периметр більшим – завжди множте на масштаб.
Ці помилки, хоч і поширені, легко уникнути з практикою, і вони додають шар реалізму до математики, ніби нагадують, що навіть прості речі вимагають уваги.
Просунуті методи: периметр через координати та вектори
Для просунутих ентузіастів периметр квадрата можна знайти через координатну геометрію, ніби малюєте його на графіку. Якщо вершини в точках (0,0), (a,0), (a,a), (0,a), то відстані між ними – a кожна, P = 4a. Це корисно в програмуванні, де алгоритми, як у Python, обчислюють це автоматично.
Векторний підхід: сторони як вектори з однаковою довжиною, периметр – сума модулів. Якщо вектор сторони |v| = a, то P = 4|v|. У 2025 році, з AI в освіті, такі методи інтегрують у додатки, роблячи навчання інтерактивним.
Ще один рівень: у неевклідовій геометрії квадрат деформується, але периметр адаптується. Наприклад, на сфері периметр “квадрата” з великими колами – складніший, але базується на тій же ідеї суми сторін. Це розширює горизонти, ніби запрошує до космічних подорожей математики.
Історія та еволюція концепції периметра
Концепція периметра сягає Вавилону, де глиняні таблички 1800 р. до н.е. показують розрахунки для квадратних полів. Евклід у “Елементах” систематизував це, роблячи квадрат основою геометрії. У Середньовіччі арабські математики, як Аль-Хорезмі, додали алгебру, перетворюючи P = 4a на інструмент для торгівлі.
У сучасності, з 19 століття, периметр увійшов у шкільні програми, а в 2025 році – у цифрові симуляції, де VR дозволяє “обійти” квадрат віртуально. Це еволюція від паперу до екрану, ніби жива історія, що продовжує писатися.
Цікаво, як периметр вплинув на культуру: від квадратних пірамід Гізи до сучасного мистецтва Мондріана, де лінії – це периметр ідей. Розуміння цього робить математику не сухою, а частиною людського досвіду.
Практичні поради для початківців і просунутих
Почніть з візуалізації: намалюйте квадрат і позначте сторони – це закріплює формулу в пам’яті, ніби створюєте ментальну мапу. Для просунутих використовуйте калькулятори чи apps, як GeoGebra, щоб експериментувати з варіаціями.
У задачах завжди перевіряйте одиниці і контекст – чи це теоретичний квадрат, чи реальний об’єкт з товщиною? Це додає точності, роблячи ваші розрахунки надійними, ніби міцний фундамент будинку.
І пам’ятайте: математика – це гра, де периметр квадрата – лише початок. Експериментуйте, помиляйтеся, вчіться – і незабаром ви побачите квадрати скрізь, від зоряного неба до екрану телефону, де кожна піксельна рамка шепоче свою формулу.